GIZAZINEの記事をなぞってみる：「100人を部屋に集めてお金をランダムな相手に渡し続ける」とだんだんと貧富の差が生まれる

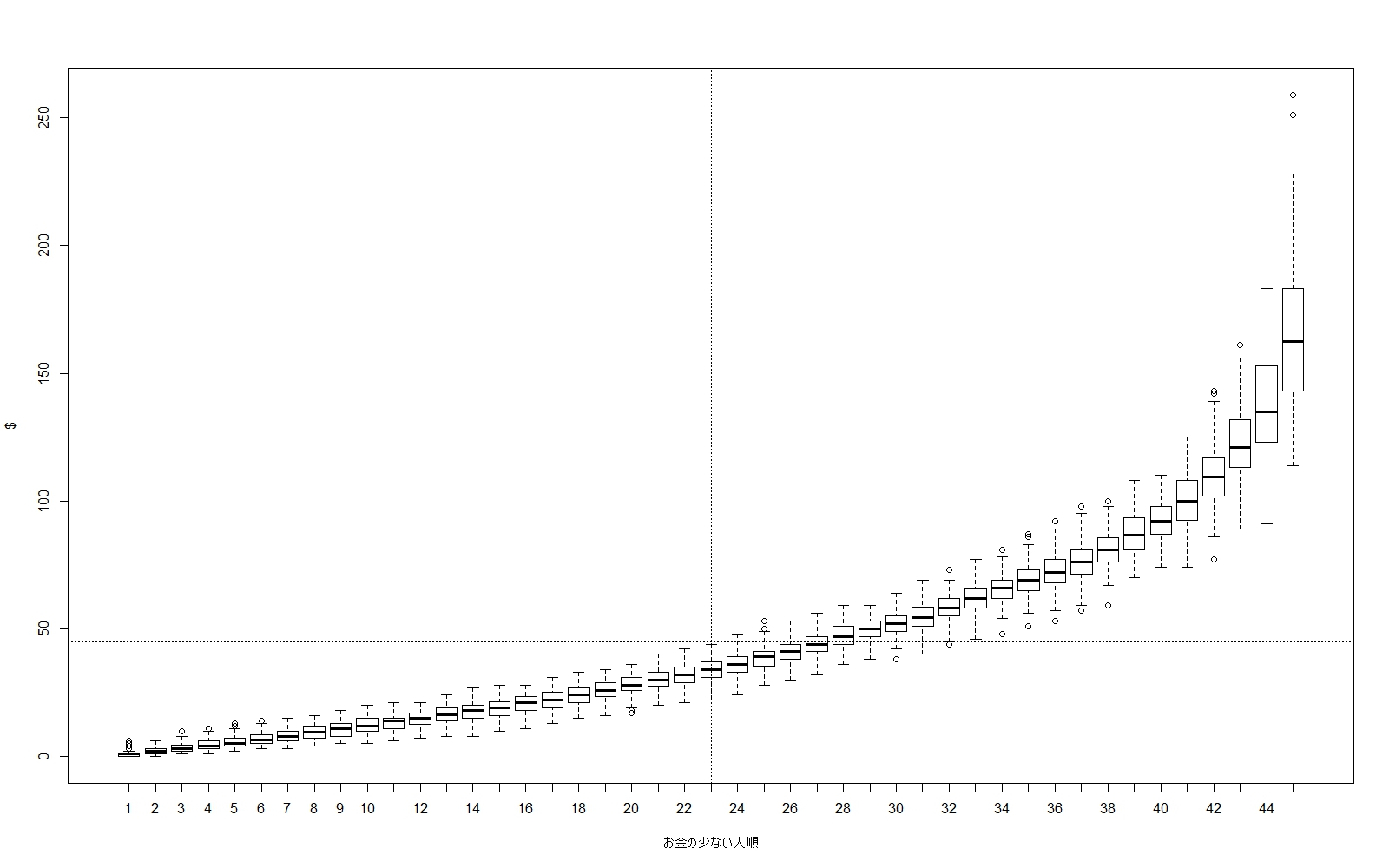
＃7/12追記　普通にソートした順でboxplotをすれば分かりやすかったので最下部に図を追加

GIGAZINEで興味深い記事が。
「100人を部屋に集めてお金をランダムな相手に渡し続ける」とだんだんと貧富の差が生まれる
というもの。

記事の中では「45ドルを持った45人が、1カウントごとに誰かに1ドル渡す」というシミュレーション」
をしているので、同じようにRでやってみる。

N <-  45  #人数
st <- 45  #初期所持ドル
turn <- 5000  #何回施行するか
SN <- 100  #シミュレーション回数

result <- matrix(0, ncol = N, nrow = SN)

for(j in seq_len(SN)){
phase <- matrix(0, ncol = N, nrow = turn+1)
phase[1,] <- 45

give <- function(x){
      non0num <- (x != 0)
      non0 <- sum(non0num)
      x <- (x - non0num)
      add <- sample(seq_len(N), non0, replace = TRUE)
      x <- x + as.numeric(table(factor(add, levels = seq_len(N))))
}

for(i in seq_len(turn)){
      phase[i + 1,] <- give(phase[i,])
}

result[j,] <- phase[turn+1, ]
cat(j, "; ")
}

hist(apply(result, 1, median))
(apply(result, 1, mean)) ##must 45
hist(apply(result, 1, max))
hist(apply(result, 1, min))

plot(0, xlim = c(0, 300), ylim = c(0, 0.03), type = "n",
     main = "density of $", ylab = "density", xlab = "$")
plot1 <- function(x) lines(density(x), xlim = c(0, 300), add = T)

apply(result, 1, plot1)

以下５０００回目の状況（中央値など）を１００回シミュレーションしたグラフ

中央値所持＄、、、多くの場合４５ドル無いんだねぇ
f:id:r-statistics-fan:20170711203732j:plain
平均所持＄（省略。当然全部４５＄）
最大所持＄、、、１５０＄オーバー当たり前なのね。３倍以上だね

最小所持＄、、、０＄の人が出て当たり前なのなー

５０００回目のざっくりした密度１００施行分
f:id:r-statistics-fan:20170711212631j:plain