Fisher's exact testが"正確”かどうか

f:id:r-statistics-fan:20171031163411j:plain

https://oku.edu.mie-u.ac.jp/~okumura/stat/fisher-chisq.html
https://twitter.com/genkuroki/status/910360137256325121

このあたりのFisher's exact testが"正確”かどうかという議論が勉強になる

それぞれの立場でそれぞれ一理ある

前提として周辺度数の固定という条件を許容するかどうか
P値について、理想の値に近いことを正確と表現するか、アルファエラーが保たれることを正確とするか
で混乱しているように思う

自分の認識は、
”サンプルサイズが少ないときはカイ二乗検定ではアルファエラーが保たれないので
Fisher's exact testを使用するべき”
です。
なぜなら、研究時に少ないNのデータで有意差を証明したとしても、もしアルファエラーが
保たれない可能性がある手法を使っていたら誰も納得しないからです。

一方、全体の状況を眺めるとき（個々の有意差が主目的ではない）などは、より理想値に近い
カイ二乗が良いと考えます。

というものの、理想の値に近く、かつ、アルファ水準が保たれる手法がベストです。
Fisher's exact testは、周辺度数が固定されない一般の状況下において、
あまりに保守的すぎるのも事実です。

結局、個別にモンテカルロシミュレーションをしてカイ二乗の分布を個別に出して
P値を計算するのが現状でのベストかなと思います。
全体を眺める際には多数の表を計算するので時間がかかりますがそっちは通常のカイ二乗で良いわけで
メインアウトカムの評価時だけなら時間がかかっても問題なし。

同じことを考えた人は恐らく多いと思うが、検索する気力はなしー。

ということで、Rで実際にやってみる。
ろくに検証しておらず載せるかどうか悩んだが、好き放題書いて批評されて
自分の勉強になることも目的の一つに敢えて匿名blogにしているのでGOサイン～。

奥村先生のコードを流用します
https://oku.edu.mie-u.ac.jp/~okumura/stat/fisher-chisq.html

素人なんで間違っていたらごめんなさい。
叩かれまくったら今度はじめて伺うJapanRで端っこの方で恥ずかしくて縮こまってますわー。

###########
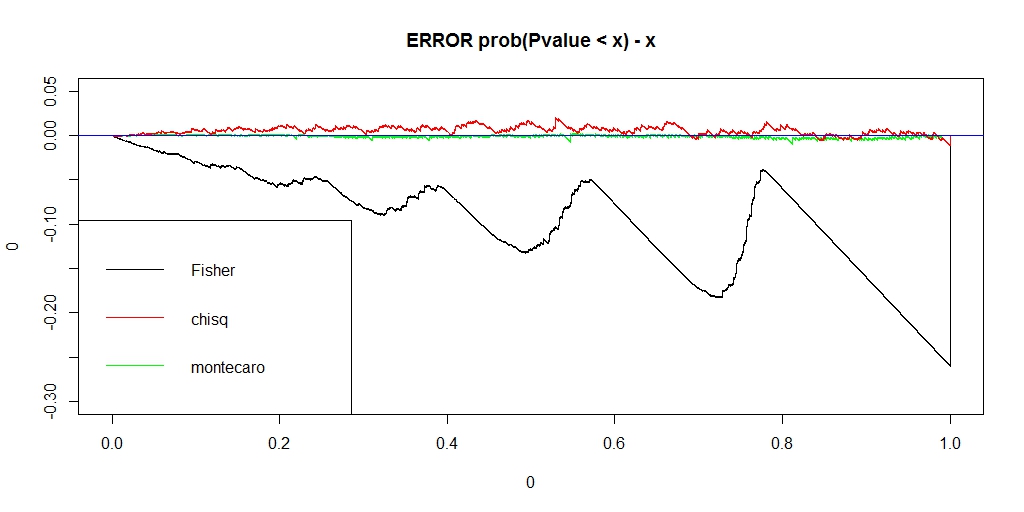
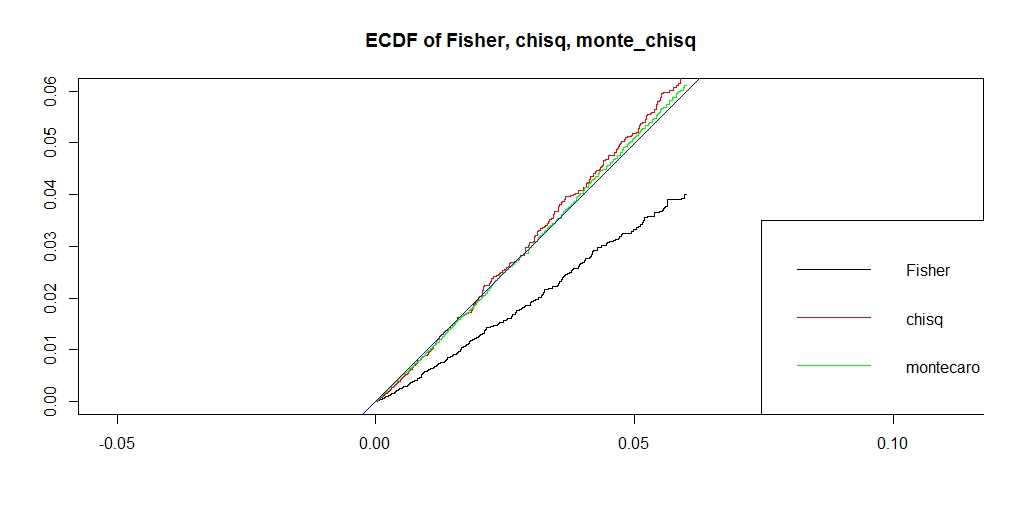
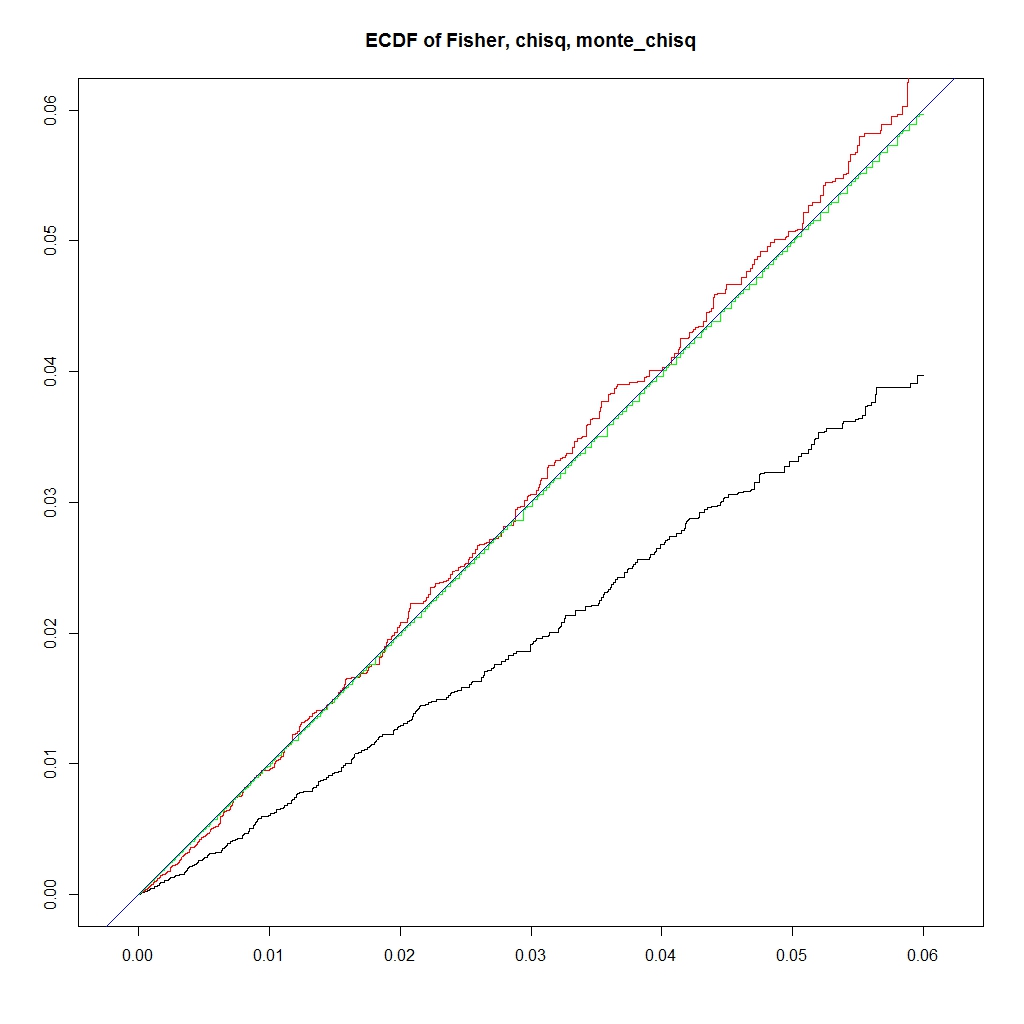
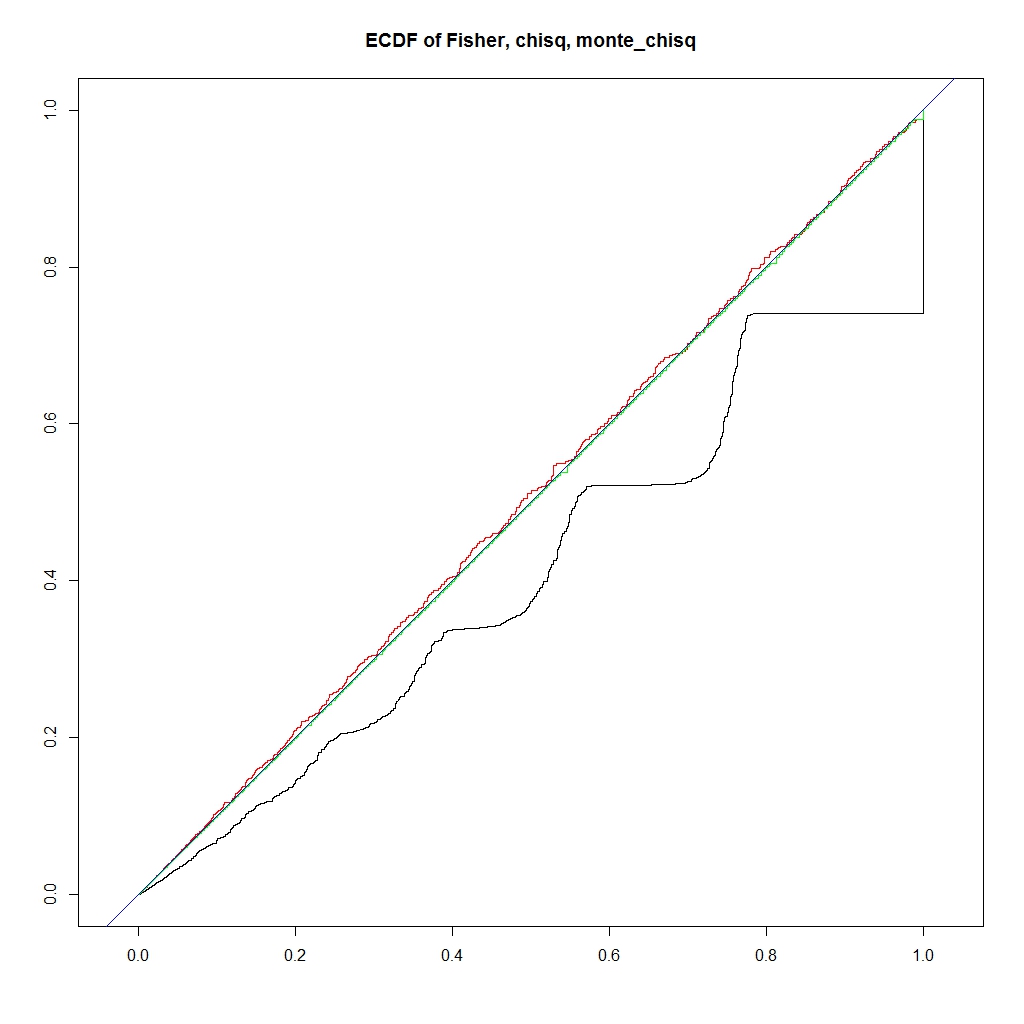
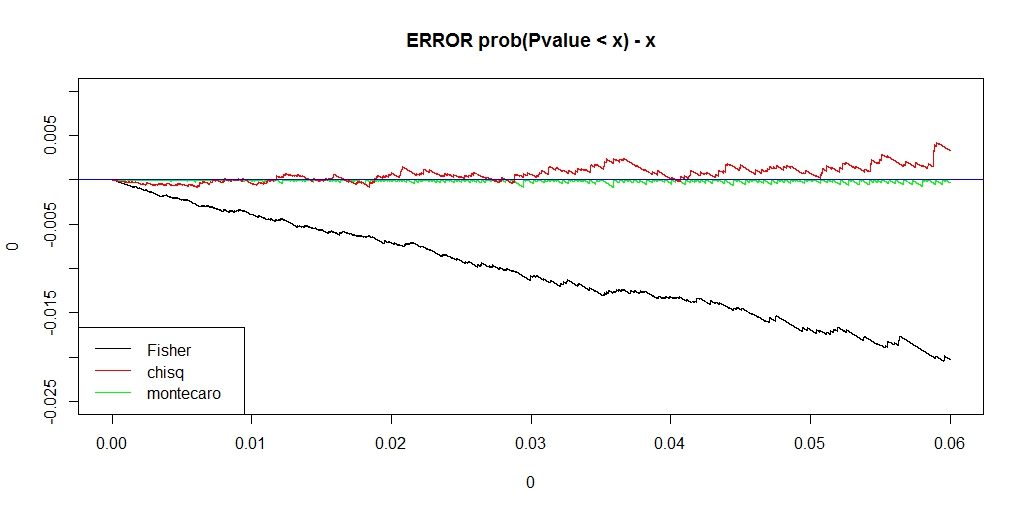
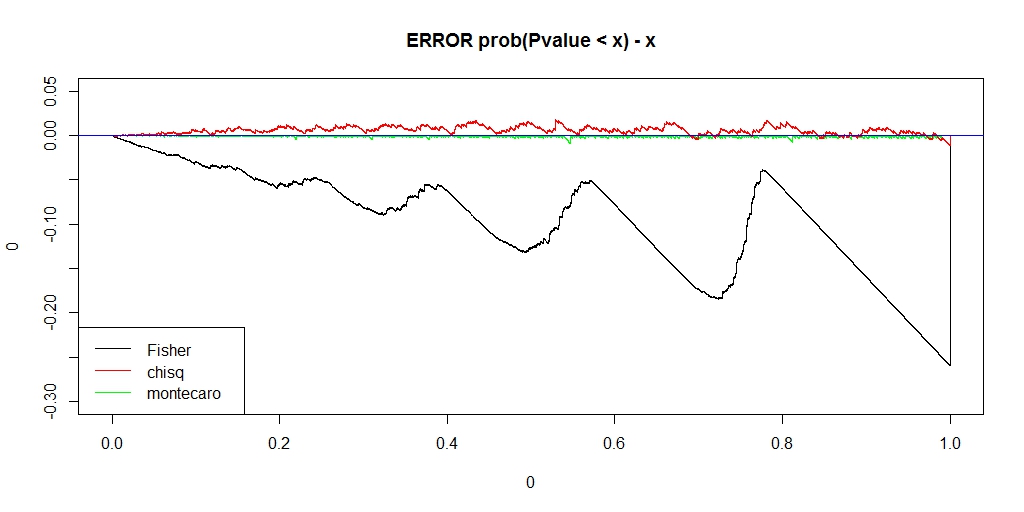
prob = c(0.12,0.18,0.28,0.42)
ni = 100000
chi = pfis = pchi = pchic = numeric(ni)
for (i in 1:ni) {
      k = sample(1:4, 50, replace=TRUE, prob=prob)
      na = sum(k == 1)
      nb = sum(k == 2)
      nc = sum(k == 3)
      nd = sum(k == 4)
      a = matrix(c(na, nb, nc, nd), nrow=2)
      pfis[i] = fisher.test(a)$p.value
      pchi[i] = chisq.test(a, correct=FALSE)$p.value
      chi[i] = chisq.test(a, correct=FALSE)$statistic
      pchic[i] = chisq.test(a, correct=TRUE)$p.value
}
ecdf_chi <- ecdf(-chi)
monte_chi_p <- ecdf_chi(-chi)
ecdf_monte_chi <- ecdf(monte_chi_p)

lim <- 0.06
ecdf_monte_pchi <- ecdf(monte_chi_p)
ecdf_pfis <- ecdf(pfis)
ecdf_pchi <- ecdf(pchi)

f0 <- function(lim){
      x1 <- seq(0, lim, length.out = length(monte_chi_p))
      plot(0, type = "n", asp=1, xlab="", ylab="", xlim=c(0,lim), ylim=c(0,lim),
   main="ECDF of Fisher, chisq, monte_chisq")
lines(x1, ecdf_pfis(x1), asp=1, xlab="", ylab="", xlim=c(0,lim), ylim=c(0,lim), type = "l",
     main="ECDF of Fisher, chisq, monte_chisq")
lines(x1, ecdf_pchi(x1), xlab="", ylab="", xlim=c(0,lim), ylim=c(0,lim),
     col = "RED")
lines(x1, ecdf_monte_pchi(x1), xlab="", ylab="", xlim=c(0,lim), ylim=c(0,lim),
     col = "GREEN")
abline(0,1, col = "blue")

legend("bottomright", legend=c("Fisher", "chisq", "montecaro"), lty =1, col = c("black", "red", "green"))
}

f0(0.06)
f0(1)



f <- function(lim, y_lim){
x1 <- seq(0, lim, length.out = length(monte_chi_p))
plot(0,0, type ="n", xlim=c(0, lim), ylim= y_lim, main = "ERROR prob(Pvalue < x) - x")
lines(x1, ecdf_monte_pchi(x1) - x1, type ="l", col = "green")
lines(x1, ecdf_pfis(x1) - x1, type ="l", col = "black")
lines(x1, ecdf_pchi(x1) - x1, type ="l", col = "red")
abline(h=0, col = "blue")

legend("bottomleft", legend=c("Fisher", "chisq", "montecaro"), lty =1, col = c("black", "red", "green"))
}

f(0.06,c(-0.025, 0.01))
f(1, c(-0.3, 0.05))