対応の壊れたゲーム結果を復元する
対応の壊れたゲーム結果を復元する
対応の壊れたゲーム結果を復元する - ryamadaの遺伝学・遺伝統計学メモ
ここで、面白そうな問題が出ていた。
ボーリングの第一ゲームは、各人のスコアが分かっている。
第二ゲーム以降は、どのスコアが誰のものなのか分からなくなったという設定。
第二ゲーム以降、どのスコアが誰のものか推定するというもの。
通常、どこに差があって、どのように意味があるか?を解析することが多い。 しかし、この問題は、差があるものではなく、同じもののペアを探索する。 いつもと勝手が違い、最適な方法はよく分からない。だが、練習も兼ねて出来る範囲でやってみる。 4回のゲームだが、それぞれ順番が独立してランダムのため、 2回のゲームだけで検討することにした。 まあ、3,4回目のゲームの結果を2回めのゲームの割り振りに 役立てる方法が自分では考えつかなかったというだけだが。
分布が近い物同士をペアにする考えで行く。 適切かどうかは分からないが、KS-p-valueが一番大きいものを 優先的にペアにする方針とする。KS-P値が同じ中では平均値が近いもの にする。本当はすべての組合せを検討したかったが、12!は 大きすぎた。あるていどペアを作ったら、総当りにするアルゴ リズムも検討したが、夜勤明けで眠気の限界に達し断念した。
平均値の差だけとか、Uテストだけとかだと、正解数は12個のうち、メジアン4が限界だった。一応試した中ではこれがメジアン5、平均4.9で一番良かった。ランダムならメジアン1なので、まあまあかな。しかし、一番最初に完成したバージョンが一番よい結果を出すとは。その後の苦労は何だったのか(ここには載せてないけど、見通しが良いコードになって分かりやすくなったのにパフォーマンスが低下した)。
# ボーリング library(tcltk)
set.seed(1)
n.player <- 12
n.game <- 2 #1ゲーム分のみ予測することにする
n.pitch <- 10
niter <- 2
good <- numeric(niter)
for (ii in 1:niter) {
# pb <- txtProgressBar(min=1, max=niter, style=3) setTxtProgressBar(pb, ii)
m <- runif(n.player) * 10
v <- runif(n.player) * 5
my.scores <- array(0, c(n.game, n.player, n.pitch))
for (i in 1:n.game) {
for (j in 1:n.player) {
for (k in 1:n.pitch) {
tmp <- round(rnorm(100, m[j], v[j]))
tmp. <- tmp[which(tmp >= 0 & tmp <= 10)]
my.scores[i, j, k] <- tmp.[1]
}
}
}
rnd <- sample(1:n.player)
# rnd = 3 6 11
# ,,,ならば、game1の3番目が game2の1番目になる g1の6番がg2の2番目
my.scores[2, , ] <- my.scores[2, rnd, ]
res.t <- res <- matrix(0, nrow = n.player, ncol = n.player)
for (j in 1:n.player) {
for (k in 1:n.player) {
res[j, k] <- ks.test(my.scores[1, j, ], my.scores[2, k, ], alternative = "two.sided",
exact = FALSE)$p.value
}
}
# my.scores [game, player, pitch] res [game1.player, game2の順番 ]
ans.t <- ans <- check <- numeric(n.player)
temp <- temp.2 <- temp.3 <- numeric(0)
res2 <- numeric(n.player)
for (i in 1:n.player) {
res2[i] <- which.max(res[i, ])
}
tbl <- table(res2)
tbl <- tbl[tbl == 1]
temp <- as.integer(names(tbl)) #game 2 でtemp番目の人は確定
for (i in temp) {
check[res2[which(res2 == i)]] <- which(res2 == i) #一番よい数値が単独だったものは確定にする
ans[res2 == i] <- i
}
# 平均値を使った割り振り
tbl <- table(res2)
tbl <- tbl[tbl != 1]
onaji <- as.integer(names(tbl)) #game 2 でtemp番目の人は確定
for (i in onaji) {
onaji.1 <- which(res2 == i)
temp.4 <- numeric(length(onaji.1))
cnt <- 0
for (j in onaji.1) {
cnt <- cnt + 1
temp.4[cnt] <- abs(mean(my.scores[2, i, ]) - mean(my.scores[1, j,
]))
}
check[res2[onaji.1[which.min(temp.4)]]] <- onaji.1[which.min(temp.4)]
}
temp.2 <- which(check != 0) #確定の人game 2 no.
temp.3 <- which(check == 0) #未確定の人game 2 no.
mikaku <- setdiff(1:n.player, check) #未確定の人 game1 no.
for (i in temp.3) {
check[i] <- mikaku[which.max(res[mikaku, i])]
mikaku <- mikaku[mikaku != mikaku[which.max(res[mikaku, i])]]
temp.3 <- temp.3[temp.3 != i]
temp.2 <- setdiff(1:n.player, temp.3)
}
good[ii] <- sum((check - rnd) == 0)
}
hist(good, breaks = c(seq(-0.5, 12.5, by = 1)))
> median(good)
[1] 5
> mean(good)
[1] 4.939
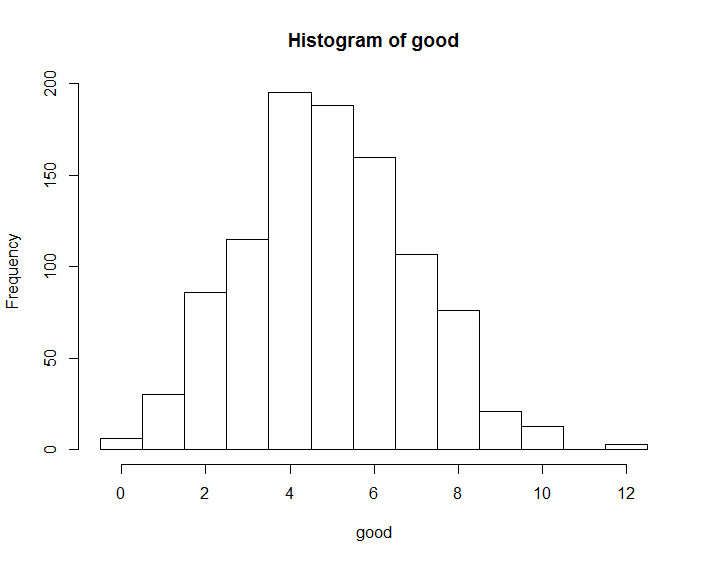
ちなみに、ランダムに割り振るとこんな感じ。
# ランダムなら
miter <- 10000
ch <- 1:n.player
rndm <- numeric(miter)
for (i in 1:miter) {
rn <- sample(ch)
rndm[i] <- sum((ch - rn) == 0)
}
hist(rndm, breaks = c(seq(-0.5, 12.5, by = 1)))
median(rndm)
## [1] 1
mean(rndm)
## [1] 1.001
ランダムなら1個しか合わないところが、5まで高まった。
今日はこれでおしまい。 ランダムよりはきちんと予測できている。