シングルアームの生存率解析デザイン（２）信頼区間の真値カバー率

信頼区間の真値カバー率をシミュレーションする。

ここ
http://www.sascom.jp/download/pdf/usergroups11_A-02.pdf
で、シミュレーションされているが、前提によってデコボコとカバー率が変わる。
平均的に、loglogが良さそうという話であった。

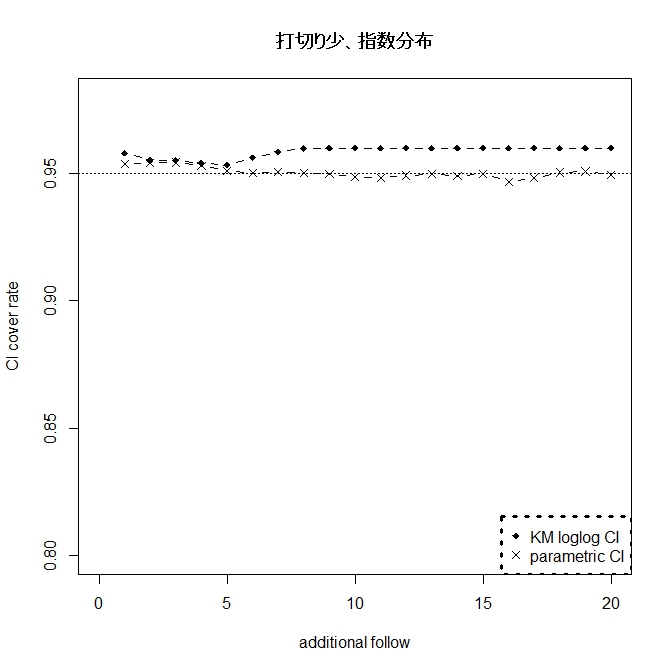
今回は、指数分布のパラメトリックな方法の信頼区間　vs　カプランマイヤー（KM)loglogの
信頼区間でのカバー率対決である。生存率はいろいろ変えていないので、あくまで一例。
デコボコのボコの部分である可能性も残るのであしからず（やったすべての解析を示し
ている。決して都合の良い物を選んでは無いことは明記しておく。）。

各前提で、10000回ずつシミュレートした。
登録期間２４ヶ月（月２人ペース）、脱落率年５％。
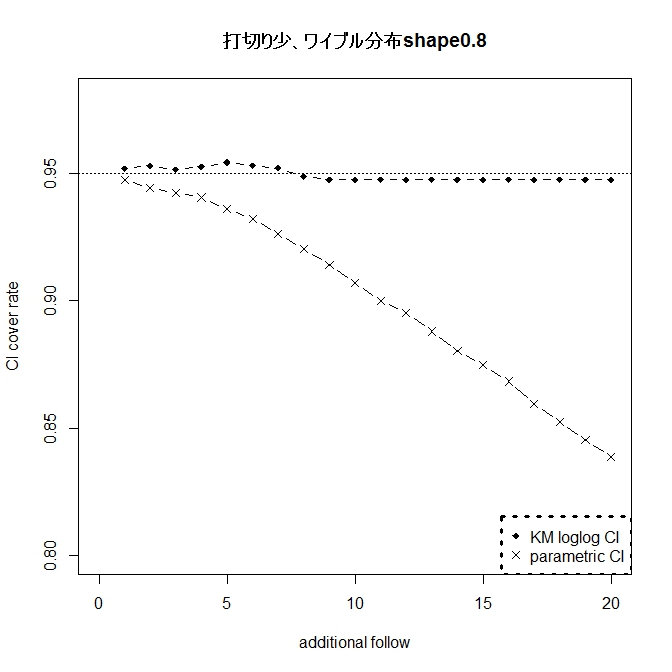
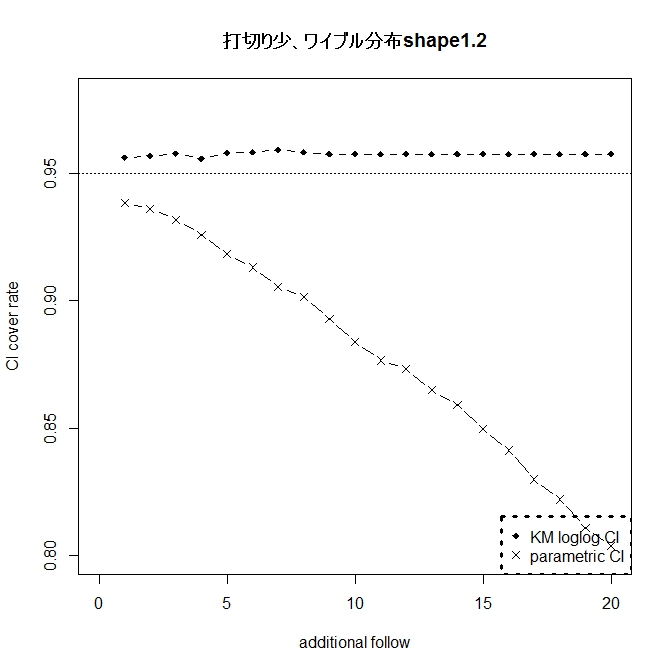
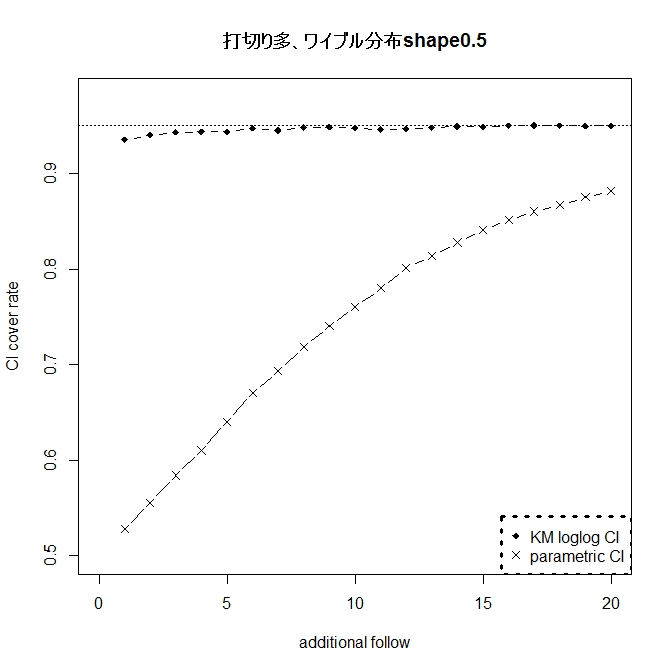
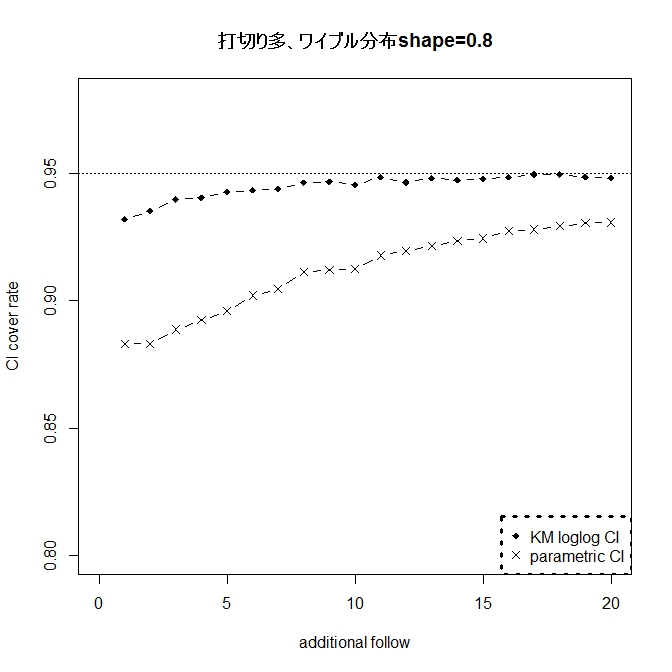
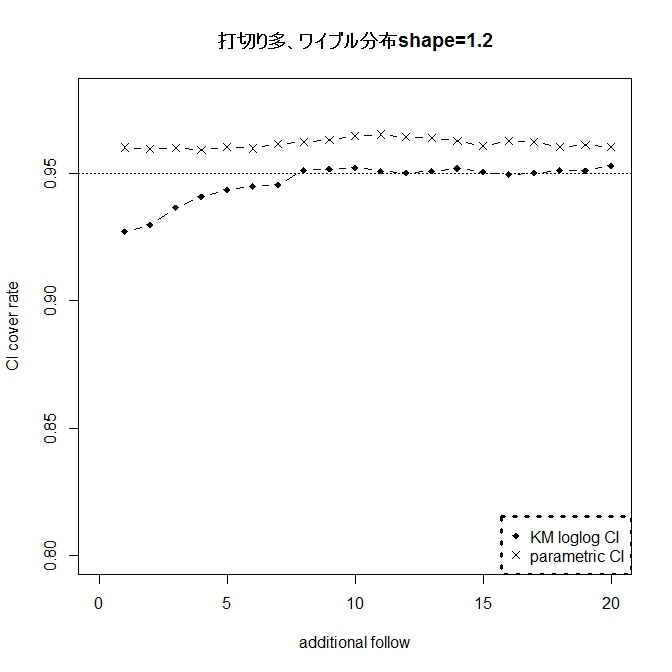
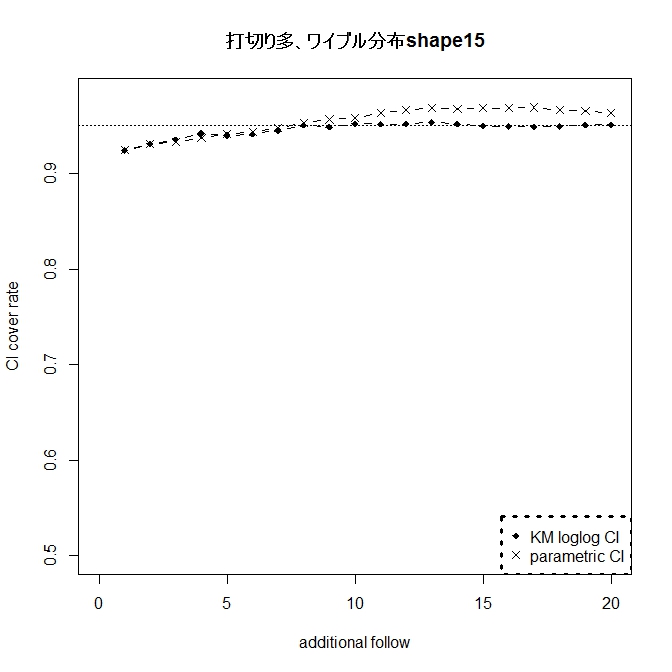
指数分布の場合２４ヶ月生存率0.5に設定。指数分布からズレる場合はワイブル分布の
shape=0.5，0.8、1.2、1.5とした。
９ヶ月あるいは２４ヶ月の時点での真値のカバー率をシミュレートしている。
解析のタイミングは２４ヶ月＋更にそこから最大20ヶ月分をシミュレートした。
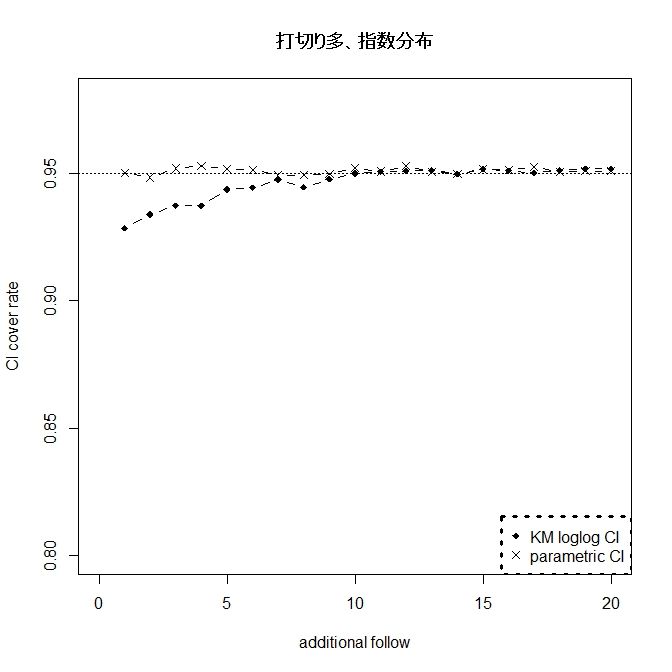
したがって、フォロー期間が長くなればなるほど（グラフでは右側）、打切り例は少なくなる。

結論：

カプランマイヤーは指数分布からのズレに強くロバスト。だが、Powerは劣る。
平均的には上記リンクのように、
loglogの信頼区間は打切り例が多くてもロバスト。

一方、正しく指数分布ならば、パラメトリックな方法は信頼区間は正確であり、
Powerも高くなり一番推奨されると思われる。まさに最強。
ただし、指数分布からズレていると、極めて怪しい結果となる。ズレによっては
差がなくても簡単に有意差が出せそうなレベルであった。

と、いうことを念頭に置いて、パラメトリックな解析結果は見る必要がある。
有意差があっても眉唾のこともあるかもね。