さや香の見せ算をRで実装する(点対称、線対称を考慮する)
M1楽しかった。
さや香の見せ算をRで実装してみる。
まずは、見せ算を考察する
2と5を見間違うわけだから、あまり目はあまり良くない
そして、おそらくデジタルの数字であろう
なので、デジタルの1と、逆さになったデジタルの1は同じと判定されるだろう
0,8も同様
1と100のときに両方に含まれる1は何も考慮されておらず、個々の桁ではなく全体としての判定になっているだろう
11になるのは、点対称。6と9は回転すると完全に重ねることができる
携帯を落として1.1になる似たものは2と5=つまり線対称。そして回転しても決して重ねることはできない。
1vs100のように、100倍以上の差があれば、少ない方の一人あたり17人倒す。残った人の83人あたり1人生まれる
これで実装が可能となる
同値なら0を返す
点対称なら11
線対称なら1.1
100倍以上の差の計算
今回は交換法則は成り立つと仮定する
%見せ%という演算子で実装する
一番下にRのコードを記す
2205 %見せ% 5022 なら、点対称なので完全に重なるため11
2205 %見せ% 2055 なら、線対称なので完全には重ならず1.1
> 1 %見せ% 1 [1] 0 > 6 %見せ% 6 [1] 0 > 6 %見せ% 9 [1] 11 > 9 %見せ% 6 [1] 11 > 2 %見せ% 5 [1] 1.1 > 1 %見せ% 100 [1] 84 > 2205 %見せ% 5022 [1] 11 > 2205 %見せ% 2055 [1] 1.1 > 100 %見せ% 001 [1] 84 > 2 %見せ% 1000 [1] 977 > 10 %見せ% 1000 [1] 840
##さや香 見せ算 sen <- function(x) { # 変換ルールを表すベクトル rule <- c("0" = "0", "1" = "1", "2" = "5", "5" = "2", "8" = "8") # 入力の各桁に対して変換を行う result <- "" chars <- strsplit(as.character(x), "")[[1]] chars_rev <- rev(chars) #逆順に #while(chars_rev[1] == "0"){chars_rev <- chars_rev[-1]} #頭のゼロは許容しない for (i in 1:length(chars_rev)) { digit <- chars_rev[i] # ルールに従って変換 if (digit %in% names(rule)) { result <- paste0(result, rule[[digit]]) } else { # ルールにない場合はNを返す result <- paste0(result, "N") } } # 結果を返す return(result) } ten <- function(x) { # 変換ルールを表すベクトル rule <- c("0" = "0", "1" = "1", "2" = "2", "5" = "5", "6" = "9", "9" = "6", "8" = "8") # 入力の各桁に対して変換を行う result <- "" chars <- strsplit(as.character(x), "")[[1]] chars_rev <- rev(chars) #逆順に #while(chars_rev[1] == "0"){chars_rev <- chars_rev[-1]} #頭のゼロは許容しない for (i in 1:length(chars_rev)) { digit <- chars_rev[i] # ルールに従って変換 if (digit %in% names(rule)) { result <- paste0(result, rule[[digit]]) } else { # ルールにない場合はNを返す result <- paste0(result, "N") } } # 結果を返す return(result) } '%見せ%' <- function(x, y){ if(x > y){z=x;x=y;y=z} if(x == y){return(0)} else if(as.character(x) == ten(y)){return(11)} else if(as.character(x) == sen(y)){return(1.1)} else if(x * 100 <= y){return(y - 17 * x + floor((y - 17 * x) / 83))} #100倍以上の差のときは、小*17を倒して、残ったものの83人に1人増える else(return(max(x, y))) } 1 %見せ% 1 6 %見せ% 6 6 %見せ% 9 9 %見せ% 6 2 %見せ% 5 1 %見せ% 100 2205 %見せ% 5022 2205 %見せ% 2055 100 %見せ% 001 2 %見せ% 1000 10 %見せ% 1000
一発じゃんけんでの各数の勝率~4や5の人気が高かったら何を出せば勝率が上がる?両手の場合は?何人くらいまで対応できる?シミュレーションで考察する
先日テレビで一発じゃんけんなるものを観測した
ルール
#1~5の数を出せる(0も認めると0-5,両手だと10まで可能)
#同じ数を出した人が単独だった人のなかで最大の数を出した人が勝ち
#ただし5と1(+その他)が残っていた場合は1の勝ち
#どの数も2人以上出していた場合はあいこ
とりあえず、基本の1-5の手が出せるパターンで各数字の勝率を計算した
開発者のおっしゃる通り基本は心理戦なのですが、ここでは完全ランダムで各人1-5を選ぶ前提で計算します。
大人数で効率よくじゃんけんをする方法を検証した - 偽計数学妨害罪
参考にしたこのブログでは”5に1が勝つ”というルールが無いので今回と結果が異なってきます。
また、解析的に解く気力も能力もないため式を構築せず安易にシミュレーションで回していきます。
10万回ずつシミュレーションします。
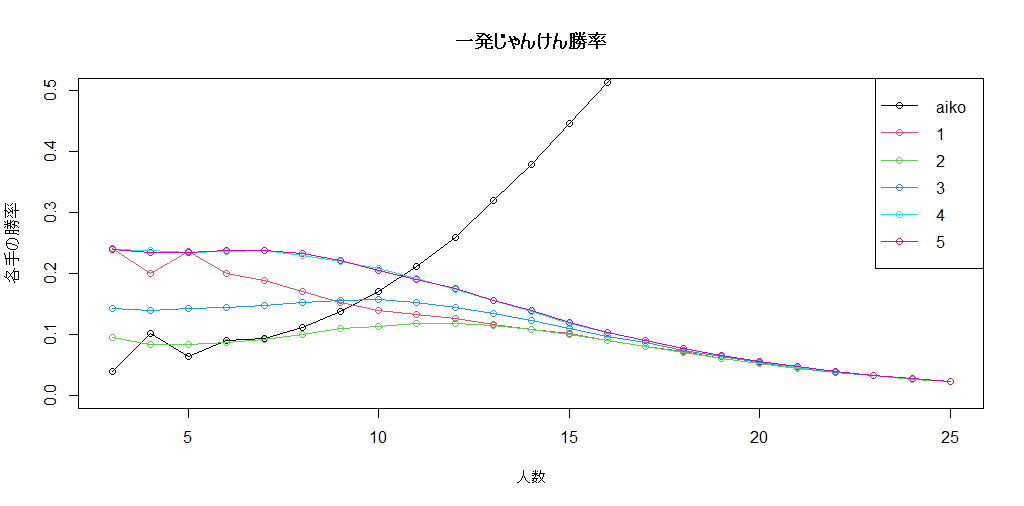
まず3~15人くらいまでの領域だと、
1は5に勝つという特権を与えられてもなお5人を超えた頃から一気に弱くなります。
2は常に弱いです。
3はいつでも中間くらい
4.5は常に強いです
ここを踏まえた上で、心理戦的に他人が選ばない数を予想するということになります。
15人超えの領域からは数字の差はほとんどなく、単独なら勝ちって感じになります。
次に各数字の確率を変えてみます
上の結果を見ちゃうと、基本4,5を選ぶでしょう。
基本確率は1-5で20,20,20,20,20%ですが、
ここは1-5が20-15-20-22.5-22.5%で3万回シミュレーションしてみます
2の不人気-5%、4.5の人気を+2.5%としました。
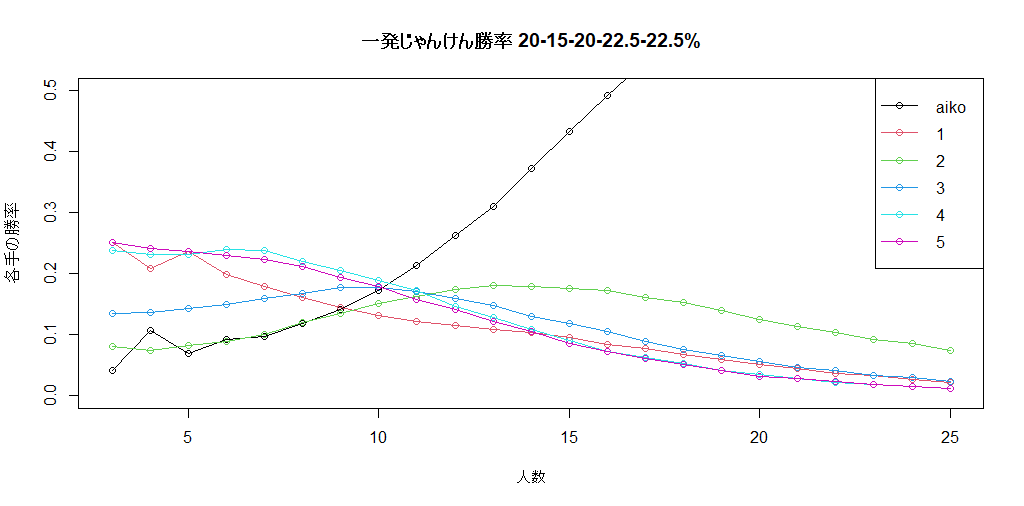
この程度だと10人を超えたころからやっと2の不人気効果が出てきます。
基本4-5が強いのなんの。
4-5好きがもっと増えた前提でもシミュレートしてみましょう
1-5が20-10-20-25-25%としてみましょう

ここまで差があっても2が強くなるのは10人を超えたあたりからです。
15人ともなると2の圧勝になります
更に4-5好きがもっと増えた前提でもシミュレートしてみましょう
1-5が15-10-15-30-30%としてみましょう

ここまで差をつけても、2は10人近くならないと強くならないですね。
かわりに15%に減ったこともあり3が7人くらいから強くなりました。
また、7人くらいから4,5は急速に弱くなります。
1-5で行う一発じゃんけんでは、少々人気不人気があっても10人くらいまでは基本4-5が強い。
10人を超えた頃から不人気数が強くなる。
これを知ったら4-5を出す人が増えるけど、めちゃくちゃ4.5が増え過ぎると3が強い気がする
黒い線はあいこですが、15人ですでに50%近くなります。全然一発じゃありません。
そこで、両手で1-10(ただし10に1が勝つ)で何人まで対応できるか計算しましょう
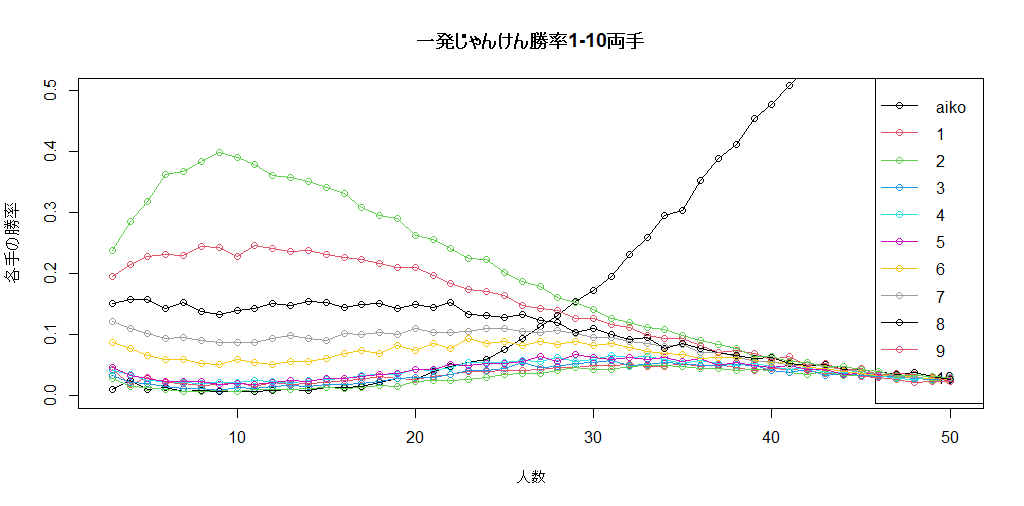
40人くらいで50%程度あいこになるので、実用上は40人あたりまででしょう。
1-5の時と比べて10の強さが際立ちますね。5以下はゴミのようだ。
二進法は非現実的なので、数えるだけでの理論上の両手の最大指、0-10でも計算してみましょう。
最低を1じゃなくて0(両手グー+グー)にするわけです。
この場合1じゃなくて、0が10に勝つことになります。
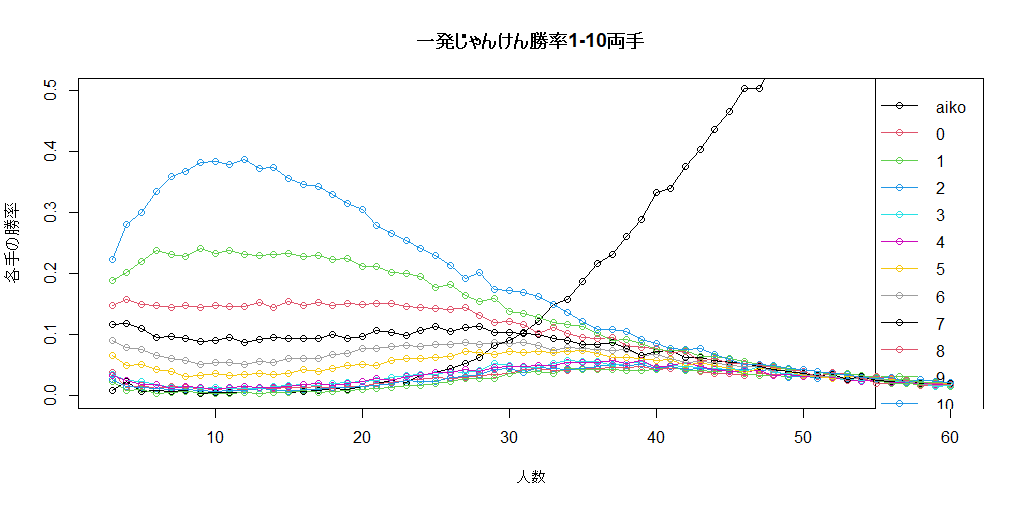
48人くらいであいこが50%ちかくになるので、更に大人数に対応できます。
やっぱり10、9、8が強いのなんの。
実生活で一発じゃんけんが使われる局面は少ないと思いますが、この知識が役立つことをお祈りいたします。
#一発じゃんけん #いっぱつじゃんけん #勝率を上げる
Rでコロナ接触アプリCOCOAのjsonデータを触ってみたい。通知されないような濃厚じゃない接触の回数も表示させる
COCOAログチェッカーが話題になっていた
GitHub - ktansai/COVID-19-ExposeChecker
cocoalog.jpcocoalog.jp
iPhoneからjson形式でCOCOAのデータをエクスポートできるようだ。
それを、COCOAログチェッカーにコピペすると”コロナすれ違い人数”とでも呼ぶべきか、濃厚じゃない接触数を表示してくれる。
これをRでやってみる。
COCOAからJSONデータがエクスポートできるので、それを保存しておく。そのCOCOAデータをR言語で読み込んて加工して出力する。
library(jsonlite)
library(RJSONIO)
library(dplyr)
library(lubridate)
ad_data <- fromJSON("ここにiPhoneからエクスポートしたファイルのパスを書く")
thresholds <- ad_data[["exposure_configuration"]][["apple_exposure_config_v2"]][["attenuation_duration_thresholds"]] #46 60 65濃厚接触判定db
score_categoly <- c(60, 150, 78, 0.6) #categoly1-4のscore
taranslation_sc <- c("1m以内", "1~2m", "1~3m", "2m以上")
alart_score <- 1350 #濃厚接触アラート
ew <- ad_data[["exposure_windows"]] #ScanInstances
TypicalAttenuationDb <- duration <- Infectiousness <- time1 <- NULL
for(i in 1:length(ew)){
time1 <- c(time1, ew[[i]]$DateMillisSinceEpoch)
Infectiousness <- c(Infectiousness, ew[[i]]$Infectiousness)
temp_ew <- ew[[i]]$ScanInstances
temp_ta <- temp_dr <- 0
for(j in 1:length(temp_ew)){
temp_dr <- temp_dr + temp_ew[[j]]["SecondsSinceLastScan"]
temp_ta <- max(temp_ta + temp_ew[[j]]["TypicalAttenuationDb"] )
}
duration <- c(duration, as.numeric(temp_dr))
TypicalAttenuationDb <- c(TypicalAttenuationDb, as.numeric(temp_ta))
}
#date1 <- as.POSIXct(time1/1000, origin = "1970-01-01", tz = "Asia/Tokyo", format = "%Y-%m-%d") ##UNIX時間をJSTに msなのでsに/1000
date1 <- as_datetime(time1/(1000), tz="Asia/Tokyo") %>% format("%Y-%m-%d")
duration <- duration / 60 #minute
dat <- data.frame(time = date1, duration = duration, TypicalAttenuationDb = TypicalAttenuationDb, Infectiousness = Infectiousness)
temp <- (table(date1))
df <- data.frame(date=names(temp), count = as.numeric(temp))
df$max_db <- df$duration <- 0
for(i in 1:nrow(df)){
df$duration[i] <- sum(dat$duration[dat$time == df$date[i]])
df$max_db[i] <- max(dat$TypicalAttenuationDb[dat$time == df$date[i]])
}
df
dat
df2 <- NULL
for(i in 1:length(ew)){
temp_time <- ew[[i]]$DateMillisSinceEpoch
temp_infect <- ew[[i]]$Infectiousness
temp_ew <- ew[[i]]$ScanInstances
temp_id <- temp_min <- temp_ta <- temp_dr <- NULL
for(j in 1:length(temp_ew)){
temp_dr <- c(temp_dr , temp_ew[[j]]["SecondsSinceLastScan"])
temp_ta <- c(temp_ta , temp_ew[[j]]["TypicalAttenuationDb"])
temp_min <- c(temp_min, temp_ew[[j]]["MinAttenuationDb"])
temp_id <- c(temp_id, i)
}
temp_df <- data.frame(SecondsSinceLastScan = temp_dr, TypicalAttenuationDb = temp_ta, MinAttenuationDb = temp_min, DateMillisSinceEpoch=temp_time,
Infectiousness = temp_infect, Count = temp_id)
df2 <- rbind(df2, temp_df)
}
df2$date <- as_datetime(df2$DateMillisSinceEpoch/(1000), tz="Asia/Tokyo") %>% format("%Y-%m-%d")
df2$minute <- df2$SecondsSinceLastScan / 60 #minute
cat_1 <- as.numeric(cut(df2$TypicalAttenuationDb, breaks = c(-Inf, thresholds, Inf), include.lowest = T, labels = 1:4, ordered_result = T,right = FALSE))
cat_2 <- as.numeric(cut(df2$MinAttenuationDb, breaks = c(-Inf, thresholds, Inf), include.lowest = T, labels = 1:4, ordered_result = T,right = FALSE))
df2$categoly_1_4 <- (cat_1 > cat_2) * cat_1 + (cat_2 >= cat_1) * cat_2
#df2$categoly_1_4 <- cat_1
df2 %>% select(date, categoly_1_4, minute, TypicalAttenuationDb, MinAttenuationDb, Count) -> df3
rownames(df3) <- NULL
df3$Score <- df2$minute * (df2$categoly_1_4 == 1) * score_categoly[1] + df2$minute * (df2$categoly_1_4 == 2) * score_categoly[2] +
df2$minute * (df2$categoly_1_4 == 3) * score_categoly[3] + df2$minute * (df2$categoly_1_4 == 4) * score_categoly[4]
df3$translation <- taranslation_sc[df3$categoly_1_4]
temp <- df3 %>% group_by(date) %>% mutate(Total_counts_day = length(unique(Count)), Count_id_day = dense_rank(Count))
#temp2 <- df3 %>% left_join(temp, by = "date", copy = TRUE)
temp3 <- temp %>% group_by(date, Count, categoly_1_4) %>%
mutate(Minutes_by_day_cat = sum(minute), Score_by_day_cat = sum(Score), Min_db = min(TypicalAttenuationDb, MinAttenuationDb),
Max_db = max(TypicalAttenuationDb, MinAttenuationDb))
temp4 <- temp3 %>% group_by(date) %>% mutate(Count_by_day = dense_rank(Count), Score_by_day = sum(Score), Minute_by_day = sum(minute),
Alrart_by_day = Score_by_day >= alart_score)
daily_log <- temp4 %>% group_by(date) %>% select(date, Alrart_by_day, Score_by_day, Minute_by_day, Total_counts_day) %>% slice(1)
day_categoly_log <- temp4 %>% group_by(date, Count, categoly_1_4) %>% select(date, Count_by_day, Minutes_by_day_cat, Score_by_day_cat,
Min_db, Max_db, translation) %>% slice(1)
print(daily_log)
print(day_categoly_log)
こんな感じになる。COCOAログチェッカーは2週間前までだが、それ以前も中にデータが有れば表示される。
cocoalog.jpとほぼ一致した。
dbの範囲が一部異なるが、こっちのほうが範囲が広いのでヨシ。
日毎の総スコアは低いのが一律60点だったり算出法がブラックボックスなので不明。日内の各スコアは一致しているのでヨシ。
> print(daily_log) # A tibble: 26 x 5 # Groups: date [26] date Alrart_by_day Score_by_day Minute_by_day Total_counts_day <chr> <lgl> <dbl> <dbl> <int> 1 2022-04-04 FALSE 12.6 21 1 2 2022-04-06 FALSE 1.8 3 1 3 2022-05-08 FALSE 1.8 3 1 4 2022-05-10 FALSE 24.6 41 4 5 2022-06-04 FALSE 1.8 3 1 6 2022-06-19 FALSE 2.4 4 1 7 2022-07-16 FALSE 3.6 6 2 8 2022-07-22 FALSE 1.8 3 1 9 2022-07-23 FALSE 3.6 6 2 10 2022-07-25 FALSE 1.8 3 1 # ... with 16 more rows > print(day_categoly_log) # A tibble: 60 x 9 # Groups: date, Count, categoly_1_4 [60] Count categoly_1_4 date Count_by_day Minutes_by_day_cat Score_by_day_cat Min_db Max_db translation <int> <dbl> <chr> <int> <dbl> <dbl> <dbl> <dbl> <chr> 1 1 4 2022-04-04 1 21 12.6 67 92 2m以上 2 2 4 2022-04-06 1 3 1.8 94 94 2m以上 3 3 4 2022-05-08 1 3 1.8 87 91 2m以上 4 4 4 2022-05-10 1 19 11.4 92 98 2m以上 5 5 4 2022-05-10 2 4 2.4 97 97 2m以上 6 6 4 2022-05-10 3 5 3 98 98 2m以上 7 7 4 2022-05-10 4 13 7.8 93 99 2m以上 8 8 4 2022-06-04 1 3 1.8 79 83 2m以上 9 9 4 2022-06-19 1 4 2.4 91 94 2m以上 10 10 4 2022-07-16 1 3 1.8 93 95 2m以上 # ... with 50 more rows
65歳から何年繰り下げると年金がお得か?~年金期待値を日本人の生命曲線から計算する
#年金 #繰り下げ #計算 #生命曲線 #期待値 #最大値
計算違いなどがあっても責任は取りかねます。実際は税金や社会保障費が余計に取られたりして単純には行きませんのでお遊びと思ってご覧ください。
既に65歳まで生きている人は、日本人平均余命(0歳の平均余命)より長生きである。
65歳からもらえる年金を繰り下げれば、より多くの年金がもらえるらしい。
しかし、もらえる前に死んでしまうリスクもある。
期待値ではどうなのだろうと疑問に。
令和二年の完全生命表から男女の生命曲線がわかるので計算できる。
Rで計算してみる
条件
基本の年金は月1とする(10万円なら10万倍してください)
月々0.7%もらえる年金が増加
生命表に従い65才以降の死亡を計算。各年の中では月々均等に死亡する。
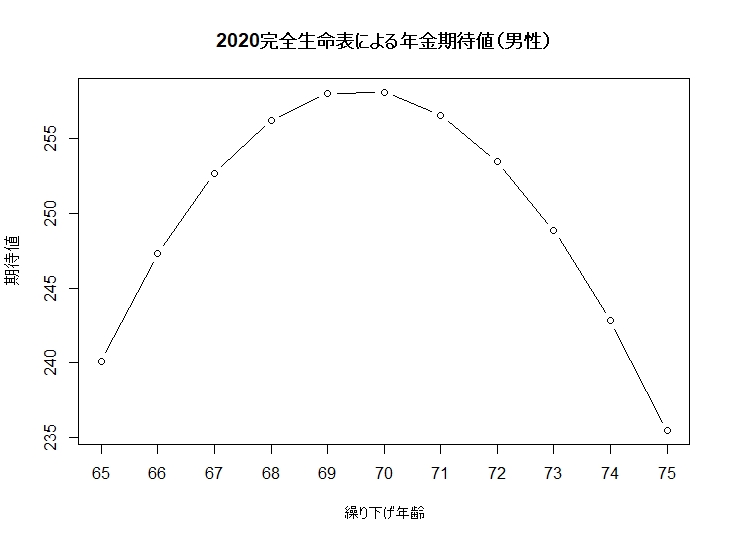


男性では70才付近、女性では72才付近が年金期待値が良さそうだ。
65歳まで生きた人の余命中央値は男性85.9歳、女性91.1歳
損益分岐点は
繰り下げなしを70才繰り下げが超えるのは81.8歳→男女ともに中央値クリア
繰り下げなしを75才繰り下げが超えるのは86.8歳→女性だけ中央値クリア
70才繰り下げを75才繰り下げが超えるのは91.8歳→男女ともに中央値クリアできず
つまり五分五分以上で損益分岐を上回れるのは、男性は70才繰り下げ。女性は75才繰り下げ。
ただし、女性で75才繰り下げにすると、70才繰り下げを上回れるのは五分五分以下。
まあ期待値から男性は70才、女性は72歳でええんとちゃうと思った次第
Rソースコードは以下
#令和2年完全生命表データ抜粋 dat<-structure(list(x=c(0,1,2,3,4,5,6,7,8,9,10,11,12, 13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28, 29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44, 45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60, 61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76, 77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92, 93,94,95,96,97,98,99,100,101,102,103,104,105,106, 107,108,109,110,111,112,113,0,1,2,3,4,5,6,7,8, 9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24, 25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40, 41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56, 57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72, 73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88, 89,90,91,92,93,94,95,96,97,98,99,100,101,102,103, 104,105,106,107,108,109,110,111,112,113,114),lx=c(1e+05, 99816,99792,99775,99764,99756,99750,99744,99739,99733, 99728,99722,99715,99706,99696,99682,99664,99642,99615, 99582,99544,99501,99452,99400,99348,99297,99248,99200, 99152,99103,99054,99003,98948,98889,98825,98759,98690, 98619,98547,98471,98388,98297,98196,98086,97965,97833, 97687,97528,97353,97161,96948,96712,96452,96167,95856, 95515,95140,94729,94280,93793,93263,92681,92041,91337, 90569,89734,88829,87838,86748,85553,84254,82840,81314, 79678,77921,76033,74002,71822,69487,67005,64365,61544, 58523,55293,51850,48204,44378,40399,36312,32179,28082, 24096,20289,16721,13450,10541,8047,5993,4349,3072,2110, 1407,909,569,345,201,113,62,32,16,8,4,2,1,1e+05, 99828,99811,99800,99791,99784,99777,99771,99765,99759, 99753,99748,99742,99735,99727,99719,99707,99693,99676, 99657,99637,99615,99593,99569,99544,99519,99494,99469, 99443,99417,99390,99363,99336,99307,99277,99242,99204, 99161,99115,99066,99012,98954,98892,98826,98752,98672, 98582,98484,98378,98261,98132,97990,97835,97668,97492, 97304,97106,96894,96669,96430,96177,95906,95613,95295, 94951,94580,94181,93747,93272,92751,92183,91555,90865, 90111,89285,88380,87383,86278,85042,83659,82108,80370, 78423,76240,73792,71052,68005,64636,60935,56898,52553, 47944,43100,38066,32936,27856,22971,18479,14477,11028, 8153,5839,4042,2700,1735,1071,633,357,192,98,47,21, 9,4,1),ndx=c(184,24,17,11,8,6,6,5,5,5,6,7,9, 11,14,17,22,28,32,38,44,49,52,52,50,49,48,48,49, 49,51,55,59,63,67,69,70,72,76,83,91,100,110,121, 132,146,160,175,192,213,236,260,285,311,341,375,411, 448,487,530,582,640,704,768,835,906,991,1090,1195, 1299,1414,1526,1636,1757,1888,2031,2180,2335,2482,2639, 2822,3021,3230,3442,3646,3826,3979,4087,4133,4098,3985, 3807,3568,3272,2909,2494,2054,1644,1277,962,703,497, 340,225,143,88,52,29,16,8,4,2,1,0,172,17,12,9, 7,7,7,6,6,5,5,6,7,8,9,11,14,17,19,20,22,23, 24,25,25,25,25,26,26,27,27,27,28,31,34,39,43,46, 50,54,58,62,67,73,81,89,98,107,117,129,142,155, 167,177,187,199,211,225,239,253,271,293,319,344,371, 399,434,475,521,569,627,690,754,826,905,996,1105, 1237,1383,1550,1738,1947,2182,2448,2740,3047,3369,3701, 4037,4345,4609,4844,5034,5130,5080,4884,4493,4002,3449, 2875,2314,1796,1343,964,664,438,276,165,94,51,26, 12,6,2,1),npx=c(0.99816,0.99976,0.99983,0.99989,0.99992, 0.99994,0.99994,0.99995,0.99995,0.99995,0.99994,0.99993, 0.99991,0.99989,0.99986,0.99982,0.99978,0.99972,0.99967, 0.99962,0.99956,0.99951,0.99948,0.99948,0.99949,0.99951, 0.99951,0.99951,0.99951,0.9995,0.99948,0.99945,0.9994, 0.99936,0.99932,0.9993,0.99929,0.99927,0.99923,0.99916, 0.99907,0.99898,0.99888,0.99877,0.99865,0.99851,0.99836, 0.99821,0.99802,0.99781,0.99757,0.99731,0.99705,0.99676, 0.99644,0.99608,0.99568,0.99527,0.99483,0.99434,0.99376, 0.99309,0.99235,0.99159,0.99078,0.9899,0.98885,0.98759, 0.98622,0.98482,0.98322,0.98157,0.97988,0.97795,0.97577, 0.97328,0.97054,0.96749,0.96428,0.96061,0.95616,0.95092, 0.9448,0.93774,0.92968,0.92063,0.91035,0.89882,0.88619, 0.87266,0.85808,0.84201,0.82414,0.80434,0.78374,0.76339, 0.74472,0.72571,0.70637,0.68671,0.66676,0.64654,0.62606, 0.60537,0.58448,0.56342,0.54223,0.52095,0.49961,0.47824, 0.4569,0.43562,0.41444,0.39342,0.99828,0.99983,0.99988, 0.99991,0.99993,0.99993,0.99993,0.99994,0.99994,0.99995, 0.99995,0.99994,0.99993,0.99992,0.99991,0.99989,0.99986, 0.99983,0.99981,0.9998,0.99978,0.99977,0.99976,0.99975, 0.99975,0.99975,0.99975,0.99974,0.99974,0.99973,0.99973, 0.99973,0.99972,0.99969,0.99965,0.99961,0.99957,0.99954, 0.9995,0.99946,0.99942,0.99937,0.99932,0.99926,0.99918, 0.99909,0.99901,0.99892,0.99881,0.99869,0.99855,0.99842, 0.99829,0.99819,0.99808,0.99796,0.99782,0.99767,0.99753, 0.99737,0.99719,0.99695,0.99667,0.99639,0.9961,0.99578, 0.99539,0.99493,0.99442,0.99387,0.99319,0.99246,0.9917, 0.99083,0.98986,0.98873,0.98736,0.98567,0.98374,0.98147, 0.97883,0.97577,0.97217,0.96789,0.96287,0.95711,0.95046, 0.94274,0.93375,0.92364,0.9123,0.89896,0.88321,0.86523, 0.84576,0.82465,0.80442,0.78345,0.76173,0.7393,0.71615, 0.69233,0.66786,0.64278,0.61713,0.59097,0.56436,0.53737, 0.51007,0.48255,0.45491,0.42724,0.39965,0.37226,0.34518 ),nqx=c(0.00184,0.00024,0.00017,0.00011,8e-05,6e-05, 6e-05,5e-05,5e-05,5e-05,6e-05,7e-05,9e-05,0.00011,0.00014, 0.00018,0.00022,0.00028,0.00033,0.00038,0.00044,0.00049, 0.00052,0.00052,0.00051,0.00049,0.00049,0.00049,0.00049, 5e-04,0.00052,0.00055,6e-04,0.00064,0.00068,7e-04,0.00071, 0.00073,0.00077,0.00084,0.00093,0.00102,0.00112,0.00123, 0.00135,0.00149,0.00164,0.00179,0.00198,0.00219,0.00243, 0.00269,0.00295,0.00324,0.00356,0.00392,0.00432,0.00473, 0.00517,0.00566,0.00624,0.00691,0.00765,0.00841,0.00922, 0.0101,0.01115,0.01241,0.01378,0.01518,0.01678,0.01843, 0.02012,0.02205,0.02423,0.02672,0.02946,0.03251,0.03572, 0.03939,0.04384,0.04908,0.0552,0.06226,0.07032,0.07937, 0.08965,0.10118,0.11381,0.12734,0.14192,0.15799,0.17586, 0.19566,0.21626,0.23661,0.25528,0.27429,0.29363,0.31329, 0.33324,0.35346,0.37394,0.39463,0.41552,0.43658,0.45777, 0.47905,0.50039,0.52176,0.5431,0.56438,0.58556,0.60658, 0.00172,0.00017,0.00012,9e-05,7e-05,7e-05,7e-05,6e-05, 6e-05,5e-05,5e-05,6e-05,7e-05,8e-05,9e-05,0.00011,0.00014, 0.00017,0.00019,2e-04,0.00022,0.00023,0.00024,0.00025, 0.00025,0.00025,0.00025,0.00026,0.00026,0.00027,0.00027, 0.00027,0.00028,0.00031,0.00035,0.00039,0.00043,0.00046, 5e-04,0.00054,0.00058,0.00063,0.00068,0.00074,0.00082, 0.00091,0.00099,0.00108,0.00119,0.00131,0.00145,0.00158, 0.00171,0.00181,0.00192,0.00204,0.00218,0.00233,0.00247, 0.00263,0.00281,0.00305,0.00333,0.00361,0.0039,0.00422, 0.00461,0.00507,0.00558,0.00613,0.00681,0.00754,0.0083, 0.00917,0.01014,0.01127,0.01264,0.01433,0.01626,0.01853, 0.02117,0.02423,0.02783,0.03211,0.03713,0.04289,0.04954, 0.05726,0.06625,0.07636,0.0877,0.10104,0.11679,0.13477, 0.15424,0.17535,0.19558,0.21655,0.23827,0.2607,0.28385, 0.30767,0.33214,0.35722,0.38287,0.40903,0.43564,0.46263, 0.48993,0.51745,0.54509,0.57276,0.60035,0.62774,0.65482 ),mux=c(0.07181,0.00048,0.00014,0.00014,9e-05,7e-05, 6e-05,6e-05,5e-05,5e-05,6e-05,7e-05,8e-05,9e-05,0.00012, 0.00015,2e-04,0.00025,3e-04,0.00035,0.00041,0.00047,0.00051, 0.00053,0.00052,5e-04,0.00049,0.00049,0.00049,0.00049, 5e-04,0.00053,0.00057,0.00062,0.00066,0.00069,0.00071, 0.00072,0.00075,8e-04,0.00088,0.00097,0.00107,0.00118, 0.00129,0.00142,0.00156,0.00171,0.00188,0.00208,0.00231, 0.00256,0.00282,0.00309,0.0034,0.00374,0.00413,0.00453, 0.00495,0.00541,0.00595,0.00658,0.0073,0.00805,0.00884, 0.00968,0.01065,0.01182,0.01317,0.01457,0.01609,0.01775, 0.01944,0.02126,0.02337,0.02576,0.02844,0.03143,0.03466, 0.03818,0.04237,0.04743,0.05339,0.06035,0.06841,0.0776, 0.08807,0.10005,0.11352,0.12829,0.14434,0.16213,0.18223, 0.20514,0.23049,0.25797,0.28219,0.30749,0.33391,0.36152, 0.39037,0.4205,0.45198,0.48487,0.51922,0.55512,0.59261, 0.63179,0.67271,0.71547,0.76013,0.8068,0.85554,0.90647, 0.06362,0.00042,7e-05,1e-04,8e-05,7e-05,7e-05,6e-05,6e-05, 6e-05,5e-05,5e-05,6e-05,7e-05,8e-05,1e-04,0.00013,0.00016, 0.00018,2e-04,0.00021,0.00022,0.00024,0.00025,0.00025, 0.00025,0.00025,0.00026,0.00026,0.00027,0.00027,0.00027, 0.00028,3e-04,0.00033,0.00037,0.00041,0.00045,0.00048, 0.00052,0.00056,6e-04,0.00065,0.00071,0.00078,0.00086, 0.00095,0.00104,0.00113,0.00125,0.00138,0.00152,0.00165, 0.00176,0.00187,0.00198,0.00211,0.00225,0.0024,0.00255, 0.00272,0.00293,0.00319,0.00348,0.00376,0.00406,0.00441, 0.00484,0.00533,0.00586,0.00648,0.00719,0.00794,0.00876, 0.00968,0.01073,0.01198,0.01353,0.01537,0.01749,0.01998, 0.02288,0.02627,0.03031,0.03511,0.04069,0.04714,0.05467, 0.06353,0.07376,0.0853,0.09872,0.11487,0.13403,0.15574, 0.18088,0.20496,0.23057,0.25782,0.2868,0.31763,0.35043, 0.38531,0.42242,0.46189,0.50388,0.54855,0.59606,0.6466, 0.70036,0.75755,0.81838,0.8831,0.95193,1.02515),nLx=c(99860, 99801,99784,99769,99760,99753,99747,99741,99736,99731, 99725,99719,99711,99701,99689,99674,99654,99629,99599, 99564,99523,99477,99426,99374,99322,99273,99224,99176, 99128,99079,99028,98976,98919,98857,98792,98724,98654, 98583,98509,98430,98343,98248,98142,98027,97900,97761, 97609,97442,97258,97056,96832,96584,96311,96014,95688, 95330,94937,94508,94040,93532,92977,92366,91694,90959, 90157,89288,88341,87302,86159,84912,83557,82086,80505, 78810,76989,75030,72924,70667,68258,65699,62970,60050, 56925,53589,50043,46305,42400,38362,34246,30124,26077, 22175,18483,15058,11963,9258,6983,5138,3682,2567,1739, 1143,728,449,267,154,85,45,23,11,5,2,1,0,99868, 99817,99806,99795,99787,99781,99774,99768,99762,99756, 99751,99745,99739,99731,99723,99713,99700,99685,99667, 99647,99626,99604,99581,99556,99531,99507,99481,99456, 99430,99403,99376,99349,99322,99292,99260,99223,99183, 99138,99091,99039,98984,98924,98859,98790,98713,98628, 98534,98432,98320,98198,98063,97914,97753,97581,97399, 97206,97001,96783,96551,96305,96043,95762,95456,95125, 94768,94383,93967,93513,93016,92471,91874,91215,90494, 89704,88839,87890,86841,85672,84363,82898,81256,79415, 77352,75040,72447,69555,66348,62814,58944,54749,50269, 45540,40595,35504,30386,25390,20687,16434,12705,9542, 6950,4900,3336,2189,1381,836,484,267,140,70,33,15, 6,2,1),Tx=c(8156116,8056256,7956455,7856671,7756902, 7657142,7557389,7457642,7357901,7258165,7158434,7058709, 6958990,6859280,6759579,6659889,6560216,6460562,6360933, 6261335,6161771,6062248,5962771,5863346,5763972,5664649, 5565377,5466152,5366976,5267849,5168770,5069742,4970766, 4871847,4772990,4674198,4575473,4476819,4378236,4279727, 4181297,4082953,3984706,3886564,3788537,3690637,3592875, 3495267,3397825,3300566,3203510,3106679,3010095,2913784, 2817770,2722082,2626752,2531814,2437307,2343266,2249734, 2156758,2064391,1972697,1881738,1791581,1702293,1613952, 1526650,1440491,1355579,1272023,1189936,1109431,1030621, 953632,878603,805678,735011,666753,601054,538084,478033, 421108,367519,317476,271171,228771,190409,156162,126038, 99961,77786,59303,44245,32283,23025,16041,10903,7221, 4654,2916,1773,1045,596,328,175,89,44,21,9,4,2,1, 8771274,8671407,8571590,8471784,8371988,8272201,8172420, 8072646,7972878,7873117,7773361,7673610,7573865,7474127, 7374395,7274672,7174959,7075258,6975574,6875907,6776260, 6676633,6577029,6477449,6377893,6278361,6178855,6079373, 5979917,5880487,5781084,5681707,5582358,5483036,5383744, 5284484,5185260,5086078,4986939,4887849,4788810,4689826, 4590902,4492043,4393253,4294540,4195913,4097379,3998947, 3900626,3802429,3704366,3606452,3508699,3411119,3313720, 3216514,3119513,3022730,2926179,2829875,2733832,2638070, 2542614,2447489,2352721,2258338,2164371,2070858,1977843, 1885371,1793497,1702282,1611788,1522084,1433245,1345356, 1258515,1172843,1088480,1005581,924326,844911,767558,692519, 620072,550517,484169,421355,362412,307662,257393,211853, 171258,135754,105368,79978,59292,42858,30153,20611,13660, 8761,5425,3235,1854,1018,534,267,127,57,24,10,4,1 ),ex=c(81.56,80.71,79.73,78.74,77.75,76.76,75.76,74.77, 73.77,72.78,71.78,70.78,69.79,68.79,67.8,66.81,65.82, 64.84,63.86,62.88,61.9,60.93,59.96,58.99,58.02,57.05, 56.08,55.1,54.13,53.16,52.18,51.21,50.24,49.27,48.3, 47.33,46.36,45.4,44.43,43.46,42.5,41.54,40.58,39.62, 38.67,37.72,36.78,35.84,34.9,33.97,33.04,32.12,31.21, 30.3,29.4,28.5,27.61,26.73,25.85,24.98,24.12,23.27,22.43, 21.6,20.78,19.97,19.16,18.37,17.6,16.84,16.09,15.36, 14.63,13.92,13.23,12.54,11.87,11.22,10.58,9.95,9.34, 8.74,8.17,7.62,7.09,6.59,6.11,5.66,5.24,4.85,4.49,4.15, 3.83,3.55,3.29,3.06,2.86,2.68,2.51,2.35,2.21,2.07,1.95, 1.83,1.73,1.63,1.54,1.45,1.37,1.3,1.23,1.16,1.1,1.05, 87.71,86.86,85.88,84.89,83.9,82.9,81.91,80.91,79.92, 78.92,77.93,76.93,75.93,74.94,73.95,72.95,71.96,70.97, 69.98,69,68.01,67.02,66.04,65.06,64.07,63.09,62.1,61.12, 60.13,59.15,58.17,57.18,56.2,55.21,54.23,53.25,52.27, 51.29,50.31,49.34,48.37,47.39,46.42,45.45,44.49,43.52, 42.56,41.6,40.65,39.7,38.75,37.8,36.86,35.92,34.99,34.06, 33.12,32.19,31.27,30.35,29.42,28.51,27.59,26.68,25.78, 24.88,23.98,23.09,22.2,21.32,20.45,19.59,18.73,17.89, 17.05,16.22,15.4,14.59,13.79,13.01,12.25,11.5,10.77, 10.07,9.38,8.73,8.1,7.49,6.91,6.37,5.85,5.37,4.92,4.5, 4.12,3.78,3.48,3.21,2.96,2.73,2.53,2.34,2.17,2.01,1.86, 1.73,1.61,1.5,1.39,1.3,1.21,1.13,1.05,0.98,0.92),sexM1=c(1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)),row.names=c(NA, -229L), class = "data.frame") ##dummy data add for long time survival curve mmax <- max(dat[dat$sexM1==1,]$x) fmax <- max(dat[dat$sexM1==0,]$x) dumage <- c((mmax+1):200, (fmax+1):200) len_d <- length(dumage) dat_dummy <- data.frame(x = dumage, lx = rep(0, len_d), ndx = rep(NA,len_d), npx= rep(NA,len_d), nqx= rep(NA,len_d), mux= rep(NA,len_d), nLx= rep(NA,len_d), Tx= rep(NA,len_d), ex= rep(NA,len_d), sexM1 = c(rep(1, length((mmax+1):200)), rep(0, length((fmax+1):200)))) dat <- rbind(dat, dat_dummy) ###年金 max_age <- 130 kurisage_rate <- 0.007 age_nenkin <- seq(65, max_age, by = 1/12) nenkin_len <- length(age_nenkin) nenkin <- seq(1, by=0.007, length.out = nenkin_len) kurisage <- function(kuri_age = 70){ temp <- rep(1, nenkin_len) flag <- which(age_nenkin == kuri_age) if(flag > 1){ temp[1:(flag-1)] <- 0 } temp[flag:length(temp)] <- nenkin[flag] return(temp) } ninnzuu <- function(sexM1F0 =1){ temp_sex <- sexM1F0 max_i <- which(dat$x[dat$sexM1 == temp_sex] == max_age) min_i <- which(dat$x[dat$sexM1 == temp_sex] == 65) temp <- NULL for(i in min_i:(max_i-1)){ temp2 <- seq(dat$lx[dat$sexM1 == temp_sex][i], dat$lx[dat$sexM1 == temp_sex][i+1], length.out = 13) temp <- c(temp, temp2[-13]) } temp <- c(temp, temp2[13]) temp <- temp / temp[1] return(temp) } exp_nenkin <- function(kuri_age = 75, sex = 1){ nenkin_tbl <- kurisage(kuri_age) cum_nen <- cumsum(nenkin_tbl) nin <- ninnzuu(sexM1F0 = sex) sibou <- -diff(nin) ex_nen <- sum(sibou * cum_nen[-length(cum_nen)]) return(ex_nen) } cal.median <- function(y, b){ #age = y #sex=b(F0M1) 以降でのmedian生存期間 #ssp <- smooth.spline(dat$lx[dat$sexM1 == b]/100000, dat$x[dat$sexM1 ==b]) #smooth spline ssp <- approxfun(dat$lx[dat$sexM1 == b]/100000, dat$x[dat$sexM1 ==b], method = "linear", rule = 2, ties = mean) #linear temp <- dat$lx[dat$sexM1 == b & dat$x == y]/100000 #return(predict(ssp, x = temp / 2)$y - y) #spline return(ssp(temp/2) - y) } ave.yomei <- function(age = 80, M1F0 = 1){ temp <- subset(dat, sexM1 == M1F0) temp$ex[temp$x == age] } cal_kurisage <- 65:75 sex <- 0 temp <- numeric(length(cal_kurisage)) for(i in 1:length(cal_kurisage)){ temp[i] <- exp_nenkin(cal_kurisage[i], sex) } plot(cal_kurisage, temp, main = "2020完全生命表による年金期待値(女性)", xlab="繰り下げ年齢", ylab="期待値", type="b", xaxt="n") axis(axis(side=1, at=65:75)) cal_kurisage <- 65:75 sex <- 1 temp <- numeric(length(cal_kurisage)) for(i in 1:length(cal_kurisage)){ temp[i] <- exp_nenkin(cal_kurisage[i], sex) } plot(cal_kurisage, temp, main = "2020完全生命表による年金期待値(男性)", xlab="繰り下げ年齢", ylab="期待値", type="b", xaxt="n") axis(axis(side=1, at=65:75)) plot(age_nenkin, cumsum(kurisage(65)), type="l", xlab="年齢", ylab="年金合計", xlim=c(65, 100)) lines(age_nenkin, cumsum(kurisage(75)), type="l", col =2) lines(age_nenkin, cumsum(kurisage(70)), type="l", col =3) abline(v = seq(70, 130, by=5), lty=2) abline(v=c(86.83333, 81.83333, 91.83333), col=2) a65_75 <- age_nenkin[min(which(cumsum(kurisage(65)) < cumsum(kurisage(75))))] #65を75が超える a65_70 <- age_nenkin[min(which(cumsum(kurisage(65)) < cumsum(kurisage(70))))] #65を70が超える a70_75 <- age_nenkin[min(which(cumsum(kurisage(70)) < cumsum(kurisage(75))))] #70を75が超える m1 <- cal.median(65, 1) + 65 #男性65歳の余命中央値 m0 <- cal.median(65, 0) + 65 #女性65歳の余命中央値 a1 <- ave.yomei(65, 1) + 65 #男性65歳の平均余命 a0 <- ave.yomei(65, 0) + 65 #女性65歳の平均余命 abline(v=c(m1, m0), col="blue") #abline(v=c(a1, a0), col="green") text(a65_75, 20, labels = paste0(round(a65_75, digits=1), "歳\n65=75"), col=2) text(a65_70, 10, labels = paste0(round(a65_70, digits=1), "歳\n65=70"), col=2) text(a70_75, 20, labels = paste0(round(a70_75, digits=1), "歳\n70=75"), col=2) text(m1, 400, labels = paste0(round(m1, digits=1), "歳\n男性中央値"), col="blue") text(m0, 400, labels = paste0(round(m0, digits=1), "歳\n女性中央値"), col="blue")
ポケモンGO 各タイプでの攻撃力上位20
すべて
Name type1 type2 ATK DEF HP CP_PL50 No
1 メガミュウツーY エスパー 426 229 235 7690 150.20
2 デオキシスA エスパー 414 46 137 2916 386.01
3 メガミュウツーX エスパー かくとう 412 222 235 7339 150.10
4 メガレックウザ ドラゴン ひこう 389 216 233 6827 384.10
5 メガフーディン エスパー 367 207 146 5099 65.10
6 ゲンシカイオーガ みず 353 268 218 6672 382.10
7 ゲンシグラードン じめん ほのお 353 268 218 6672 383.10
8 メガゲンガー ゴースト どく 349 199 155 4902 94.10
9 デオキシスN エスパー 345 115 137 3573 386.00
10 メガディアンシー いわ フェアリー 342 235 137 4913 719.10
11 メガガブリアス ドラゴン じめん 339 222 239 6132 445.10
12 メガラティオス ドラゴン エスパー 335 241 190 5661 381.10
13 メガヘラクロス むし かくとう 334 223 190 5443 214.10
14 ザシアン_けんのおう フェアリー はがね 331 240 192 5613 888.20
15 デンジュモク でんき 330 144 195 4451 796.00
16 メガバシャーモ ほのお かくとう 329 168 190 4704 257.10
17 メガサーナイト エスパー フェアリー 326 229 169 5101 282.10
18 メガエルレイド エスパー かくとう 326 230 169 5112 475.10
19 カミツルギ くさ はがね 323 182 139 4156 798.00
20 ヒヒダルマGD こおり ほのお 323 123 233 4415 555.20
21 メガジュカイン くさ ドラゴン 320 186 172 4585 254.10
22 メガリザードンY ほのお ひこう 319 212 186 5037 6.20
23 フェローチェ むし かくとう 316 85 174 3213 795.00
24 ズガドーン ほのお ゴースト 315 148 142 3727 806.00
25 メガアブソル あく 314 130 163 3732 359.10
26 メガジュペッタ ゴースト 312 160 162 4063 354.10
27 フーパ(解放) エスパー あく 311 191 173 4530 720.10
28 メガボーマンダ ドラゴン ひこう 310 251 216 5688 373.10
29 メガルカリオ かくとう はがね 310 175 172 4325 448.10
30 ブラックキュレム ドラゴン こおり 310 183 245 5206 646.10
31 ホワイトキュレム ドラゴン こおり 310 183 245 5206 646.20
32 メガバンギラス いわ あく 309 276 225 6045 248.10
33 メガカイロス むし ひこう 305 231 163 4728 127.10
34 メガスピアー むし どく 303 148 163 3824 15.10
35 ミュウツー エスパー 300 182 214 4724 150.00
36 メガメタグロス はがね エスパー 300 289 190 5552 376.10
37 ラムパルド いわ 295 109 219 3728 409.00
38 ボルトロス霊獣 でんき ひこう 295 161 188 4137 642.10
39 メガデンリュウ でんき ドラゴン 294 203 207 4799 181.10
40 イルカマン_マイティー みず 293 178 205 4481 934.10
41 メガギャラドス みず あく 292 247 216 5332 130.10
42 メガプテラ いわ ひこう 292 210 190 4655 142.10
43 アーケオス いわ ひこう 292 139 181 3766 567.00
44 ギルガルド剣 はがね ゴースト 291 97 155 2981 681.10
45 ケッキング ノーマル 290 166 284 5010 289.00
46 メガヘルガー あく ほのお 289 194 181 4344 229.10
47 メガサメハダー みず あく 289 144 172 3701 319.10
48 メガラティアス ドラゴン エスパー 289 297 190 5428 380.10
49 ランドロス霊獣 じめん ひこう 289 179 205 4434 645.10
50 レジギガス ノーマル 287 210 221 4913 486.00
くさ
Name type1 type2 ATK DEF HP CP_PL50 No
1 カミツルギ くさ はがね 323 182 139 4156 798.00
2 メガジュカイン くさ ドラゴン 320 186 172 4585 254.10
3 シェイミS くさ ひこう 261 166 225 4061 492.01
4 カプ・ブルル くさ フェアリー 249 215 172 3865 787.00
5 ロズレイド くさ どく 243 185 155 3359 407.00
6 ザルード あく くさ 242 215 233 4334 893.00
7 メガフシギバナ くさ どく 241 246 190 4181 3.10
8 キノガッサ くさ かくとう 241 144 155 2971 286.00
9 メガユキノオー くさ こおり 240 191 207 3850 460.10
10 ゴリランダー くさ 239 168 225 3758 812.00
11 アルセウス(くさ) くさ 238 238 237 4510 493.01
12 ナッシー くさ エスパー 233 149 216 3408 103.00
13 ダダリン ゴースト くさ 233 179 172 3335 781.00
14 マスカーニャ くさ あく 233 153 183 3193 908.00
15 アラブルタケ くさ あく 232 190 244 4018 979.00
16 ナッシーA くさ ドラゴン 230 153 216 3407 103.10
17 アノホラグサ くさ ゴースト 228 144 146 2745 975.00
18 ジュカイン くさ 223 169 172 3117 254.00
19 アマージョ くさ 222 195 176 3351 763.00
20 ノクタス くさ あく 221 115 172 2598 332.00
ほのお
Name type1 type2 ATK DEF HP CP_PL50 No
1 ゲンシグラードン じめん ほのお 353 268 218 6672 383.1
2 メガバシャーモ ほのお かくとう 329 168 190 4704 257.1
3 ヒヒダルマGD こおり ほのお 323 123 233 4415 555.2
4 メガリザードンY ほのお ひこう 319 212 186 5037 6.2
5 ズガドーン ほのお ゴースト 315 148 142 3727 806.0
6 メガヘルガー あく ほのお 289 194 181 4344 229.1
7 テツノドクガ ほのお どく 281 196 190 4346 988.0
8 レシラム ドラゴン ほのお 275 211 205 4565 643.0
9 メガリザードンX ほのお ドラゴン 273 213 186 4353 6.1
10 シャンデラ ゴースト ほのお 271 182 155 3695 609.0
11 イーユイ あく ほのお 269 221 146 3908 997.0
12 ウルガモス むし ほのお 264 189 198 4106 637.0
13 ヒヒダルマN ほのお 263 114 233 3511 555.0
14 メガバクーダ ほのお じめん 253 183 172 3641 323.1
15 ボルケニオン ほのお みず 252 216 190 4102 721.0
16 ファイヤー ほのお ひこう 251 181 207 3917 146.0
17 ヒードラン ほのお はがね 251 213 209 4244 485.0
18 ブーバーン ほのお 247 172 181 3541 467.0
19 ブースター ほのお 246 179 163 3424 136.0
20 ヒヒダルマD ほのお エスパー 243 202 233 4226 555.1
みず
Name type1 type2 ATK DEF HP CP_PL50 No
1 ゲンシカイオーガ みず 353 268 218 6672 382.10
2 イルカマン_マイティー みず 293 178 205 4481 934.10
3 メガギャラドス みず あく 292 247 216 5332 130.10
4 メガサメハダー みず あく 289 144 172 3701 319.10
5 パルキアO みず ドラゴン 286 223 189 4683 484.10
6 メガラグラージ みず じめん 283 218 225 4975 260.10
7 パルキア みず ドラゴン 280 215 189 4512 484.00
8 カイオーガ みず 270 228 205 4652 382.00
9 テツノツツミ こおり みず 266 211 148 3808 992.00
10 メガカメックス みず 264 237 188 4455 9.10
11 インテレオン みず 262 142 172 3351 818.00
12 ケルディオ みず かくとう 260 192 209 4181 647.00
13 ケルディオ覚悟 みず かくとう 260 192 209 4181 647.10
14 カマスジョー みず 258 127 156 3003 847.00
15 ヨワシ(群れ) みず 255 242 128 3654 746.10
16 ウーラオス(れんげき) かくとう みず 254 177 225 4077 892.00
17 ボルケニオン ほのお みず 252 216 190 4102 721.00
18 サメハダー みず あく 243 83 172 2466 319.00
19 キングラー みず 240 181 146 3198 99.00
20 アルセウス(みず) みず 238 238 237 4510 493.03
むし
Name type1 type2 ATK DEF HP CP_PL50 No
1 メガヘラクロス むし かくとう 334 223 190 5443 214.10
2 フェローチェ むし かくとう 316 85 174 3213 795.00
3 メガカイロス むし ひこう 305 231 163 4728 127.10
4 メガスピアー むし どく 303 148 163 3824 15.10
5 メガハッサム むし はがね 279 250 172 4621 212.10
6 ウルガモス むし ほのお 264 189 198 4106 637.00
7 チヲハウハネ むし かくとう 261 193 198 4102 984.00
8 クワガノン むし でんき 254 158 184 3524 738.00
9 バサギリ むし いわ 253 174 172 3557 900.00
10 ゲノセクト むし はがね 252 199 174 3791 649.00
11 ゲノセクト水 むし はがね 252 199 174 3791 649.10
12 ゲノセクト電気 むし はがね 252 199 174 3791 649.20
13 ゲノセクト炎 むし はがね 252 199 174 3791 649.30
14 ゲノセクト氷 むし はがね 252 199 174 3791 649.40
15 カイロス むし 238 182 163 3345 127.00
16 アルセウス(むし) むし 238 238 237 4510 493.04
17 ハッサム むし はがね 236 181 172 3393 212.00
18 マッシブーン むし かくとう 236 197 216 3922 794.00
19 ヘラクロス むし かくとう 234 179 190 3506 214.00
20 メガヤンマ むし ひこう 231 156 200 3330 469.00
ノーマル
Name type1 type2 ATK DEF HP CP_PL50 No
1 ケッキング ノーマル 290 166 284 5010 289.00
2 レジギガス ノーマル 287 210 221 4913 486.00
3 メガミミロップ ノーマル かくとう 282 214 163 4234 428.10
4 メガピジョット ノーマル ひこう 280 175 195 4160 18.10
5 メロエッタS ノーマル かくとう 269 188 225 4426 648.10
6 ポリゴンZ ノーマル 264 150 198 3693 474.00
7 ゾロアークH ノーマル ゴースト 261 128 146 2957 571.10
8 メロエッタV ノーマル エスパー 250 225 225 4490 648.00
9 メガガルーラ ノーマル 246 210 233 4353 115.10
10 ガチグマ じめん ノーマル 243 181 277 4358 901.00
11 アルセウス ノーマル 238 238 237 4510 493.00
12 アルセウス(ノーマル) ノーマル 238 238 237 4510 493.05
13 リングマ ノーマル 236 144 207 3329 217.00
14 ムクホーク ノーマル ひこう 234 140 198 3194 398.00
15 ウォーグル ノーマル ひこう 232 152 225 3491 628.00
16 ジジーロン ノーマル ドラゴン 231 164 186 3294 780.00
17 ケンホロウ ノーマル ひこう 226 146 190 3091 521.00
18 キテルグマ ノーマル かくとう 226 141 260 3524 760.00
19 ザングース ノーマル 222 124 177 2733 335.00
20 ドデカバシ ノーマル ひこう 222 146 190 3040 733.00
あく
Name type1 type2 ATK DEF HP CP_PL50 No
1 メガアブソル あく 314 130 163 3732 359.1
2 フーパ(解放) エスパー あく 311 191 173 4530 720.1
3 メガバンギラス いわ あく 309 276 225 6045 248.1
4 メガギャラドス みず あく 292 247 216 5332 130.1
5 メガヘルガー あく ほのお 289 194 181 4344 229.1
6 メガサメハダー みず あく 289 144 172 3701 319.1
7 ダークライ あく 285 198 172 4227 491.0
8 イーユイ あく ほのお 269 221 146 3908 997.0
9 パオジアン あく こおり 261 167 190 3764 995.0
10 サザンドラ あく ドラゴン 256 188 211 4098 635.0
11 トドロクツキ ドラゴン あく 255 178 213 3999 985.0
12 ウーラオス(いちげき) かくとう あく 254 177 225 4077 892.1
13 バンギラス いわ あく 251 207 225 4335 248.0
14 ゾロアーク あく 250 127 155 2907 571.0
15 イベルタル あく ひこう 250 185 246 4275 717.0
16 テツノコウベ あく ひこう 249 179 214 3929 990.0
17 アブソル あく 246 120 163 2856 359.0
18 サメハダー みず あく 243 83 172 2466 319.0
19 ドンカラス あく ひこう 243 103 225 3065 430.0
20 マニューラ あく こおり 243 171 172 3397 461.0
どく
Name type1 type2 ATK DEF HP CP_PL50 No
1 メガゲンガー ゴースト どく 349 199 155 4902 94.10
2 メガスピアー むし どく 303 148 163 3824 15.10
3 テツノドクガ ほのお どく 281 196 190 4346 988.00
4 ムゲンダイナ どく ドラゴン 278 192 268 5007 890.00
5 アーゴヨン どく ドラゴン 263 159 177 3587 804.00
6 ゲンガー ゴースト どく 261 149 155 3254 94.00
7 オオニューラ かくとう どく 259 158 190 3643 903.00
8 ムゲンダイナ_無限大max どく ドラゴン 250 505 452 9220 890.10
9 ウツロイド いわ どく 249 210 240 4465 793.00
10 キラフロル いわ どく 246 177 195 3700 967.00
11 ロズレイド くさ どく 243 185 155 3359 407.00
12 メガフシギバナ くさ どく 241 246 190 4181 3.10
13 アルセウス(どく) どく 238 238 237 4510 493.07
14 ブロロローム はがね どく 229 168 190 3337 943.00
15 エンニュート どく ほのお 228 130 169 2802 758.00
16 ストリンダー_ハイ でんき どく 224 140 181 2941 849.00
17 ストリンダー_ロー でんき どく 224 140 181 2941 849.10
18 ストリンダーDM でんき どく 224 140 181 2941 849.20
19 ゴースト ゴースト どく 223 107 128 2219 93.00
20 ハリーマン あく どく 222 171 198 3330 904.00
でんき
Name type1 type2 ATK DEF HP CP_PL50 No
1 デンジュモク でんき 330 144 195 4451 796.00
2 ボルトロス霊獣 でんき ひこう 295 161 188 4137 642.10
3 メガデンリュウ でんき ドラゴン 294 203 207 4799 181.10
4 メガライボルト でんき 286 179 172 4048 310.10
5 ゼクロム ドラゴン でんき 275 211 205 4565 644.00
6 ボルトロス化身 でんき ひこう 266 164 188 3782 642.00
7 ミライドン でんき ドラゴン 263 223 205 4491 999.00
8 クワガノン むし でんき 254 158 184 3524 738.00
9 サンダー でんき ひこう 253 185 207 3987 145.00
10 ゼラオラ でんき 252 177 204 3865 807.00
11 カプ・コケコ でんき フェアリー 250 181 172 3582 785.00
12 レジエレキ でんき 250 125 190 3169 894.00
13 テツノイバラ いわ でんき 250 200 225 4250 991.00
14 エレキブル でんき 249 163 181 3481 466.00
15 スナノケガワ でんき じめん 244 195 198 3867 981.00
16 ライコウ でんき 241 195 207 3902 243.00
17 ジバコイル でんき はがね 238 205 172 3623 462.00
18 アルセウス(でんき) でんき 238 238 237 4510 493.08
19 サンダース でんき 232 182 163 3265 135.00
20 レントラー でんき 232 156 190 3265 405.00
じめん
Name type1 type2 ATK DEF HP CP_PL50 No
1 ゲンシグラードン じめん ほのお 353 268 218 6672 383.10
2 メガガブリアス ドラゴン じめん 339 222 239 6132 445.10
3 ランドロス霊獣 じめん ひこう 289 179 205 4434 645.10
4 メガラグラージ みず じめん 283 218 225 4975 260.10
5 グラードン じめん 270 228 205 4652 383.00
6 ガブリアス ドラゴン じめん 261 193 239 4479 445.00
7 ランドロス化身 じめん ひこう 261 182 205 4057 645.00
8 ドリュウズ じめん はがね 255 129 242 3667 530.00
9 メガバクーダ ほのお じめん 253 183 172 3641 323.10
10 マンムー こおり じめん 247 146 242 3763 473.00
11 スナノケガワ でんき じめん 244 195 198 3867 981.00
12 ガチグマ じめん ノーマル 243 181 277 4358 901.00
13 ドサイドン じめん いわ 241 190 251 4221 464.00
14 アルセウス(じめん) じめん 238 238 237 4510 493.09
15 ワルビアル じめん あく 229 158 216 3444 553.00
16 イダイナキバ じめん かくとう 227 190 229 3821 978.00
17 テツノワダチ じめん はがね 227 216 207 3869 986.00
18 サイドン じめん いわ 222 171 233 3594 112.00
19 ゴルーグ じめん ゴースト 222 154 205 3226 623.00
20 ドンファン じめん 214 185 207 3407 232.00
こおり
Name type1 type2 ATK DEF HP CP_PL50 No
1 ヒヒダルマGD こおり ほのお 323 123 233 4415 555.2
2 ブラックキュレム ドラゴン こおり 310 183 245 5206 646.1
3 ホワイトキュレム ドラゴン こおり 310 183 245 5206 646.2
4 テツノツツミ こおり みず 266 211 148 3808 992.0
5 ヒヒダルマGN こおり 263 114 233 3511 555.3
6 パオジアン あく こおり 261 167 190 3764 995.0
7 セグレイブ ドラゴン こおり 255 167 229 4017 951.0
8 メガオニゴーリ こおり 252 168 190 3651 362.1
9 マンムー こおり じめん 247 146 242 3763 473.0
10 キュレム ドラゴン こおり 246 170 245 4041 646.0
11 ブリザポス こおり 246 223 225 4404 896.0
12 マニューラ あく こおり 243 171 172 3397 461.0
13 メガユキノオー くさ こおり 240 191 207 3850 460.1
14 グレイシア こおり 238 205 163 3535 471.0
15 アルセウス(こおり) こおり 238 238 237 4510 493.1
16 ツンベアー こおり 233 152 216 3439 614.0
17 ケケンカニ かくとう こおり 231 138 219 3286 740.0
18 モスノウ こおり むし 230 155 172 3084 873.0
19 ルージュラ こおり エスパー 223 151 163 2888 124.0
20 バイバニラ こおり 218 184 174 3190 584.0
フェアリー
Name type1 type2 ATK DEF HP CP_PL50 No
1 メガディアンシー いわ フェアリー 342 235 137 4913 719.10
2 ザシアン_けんのおう フェアリー はがね 331 240 192 5613 888.20
3 メガサーナイト エスパー フェアリー 326 229 169 5101 282.10
4 ラブトロス化身 フェアリー ひこう 281 162 179 3873 905.00
5 ハバタクカミ ゴースト フェアリー 280 235 146 4179 983.00
6 テツノブジン フェアリー かくとう 279 171 179 3943 993.00
7 カプ・テテフ エスパー フェアリー 259 208 172 3950 786.00
8 ザシアン フェアリー はがね 254 236 192 4329 888.00
9 ザシアン_ゆうしゃ フェアリー 254 236 192 4329 888.10
10 ゼルネアス フェアリー 250 185 246 4275 716.00
11 カプ・コケコ でんき フェアリー 250 181 172 3582 785.00
12 ラブトロス霊獣 フェアリー ひこう 250 201 179 3830 905.10
13 カプ・ブルル くさ フェアリー 249 215 172 3865 787.00
14 マギアナ はがね フェアリー 246 225 190 4087 801.00
15 フラエッテAZ フェアリー 243 217 179 3864 670.10
16 アルセウス(フェアリー) フェアリー 238 238 237 4510 493.11
17 サーナイト エスパー フェアリー 237 195 169 3497 282.00
18 ブリムオン エスパー フェアリー 237 182 149 3198 858.00
19 アシレーヌ みず フェアリー 232 195 190 3618 730.00
20 オーロンゲ あく フェアリー 227 139 216 3222 861.00
かくとう
Name type1 type2 ATK DEF HP CP_PL50 No
1 メガミュウツーX エスパー かくとう 412 222 235 7339 150.1
2 メガヘラクロス むし かくとう 334 223 190 5443 214.1
3 メガバシャーモ ほのお かくとう 329 168 190 4704 257.1
4 メガエルレイド エスパー かくとう 326 230 169 5112 475.1
5 フェローチェ むし かくとう 316 85 174 3213 795.0
6 メガルカリオ かくとう はがね 310 175 172 4325 448.1
7 メガミミロップ ノーマル かくとう 282 214 163 4234 428.1
8 テツノブジン フェアリー かくとう 279 171 179 3943 993.0
9 メロエッタS ノーマル かくとう 269 188 225 4426 648.1
10 マーシャドー かくとう ゴースト 265 190 207 4217 802.0
11 コライドン かくとう ドラゴン 263 223 205 4491 998.0
12 チヲハウハネ むし かくとう 261 193 198 4102 984.0
13 テラキオン いわ かくとう 260 192 209 4181 639.0
14 ケルディオ みず かくとう 260 192 209 4181 647.0
15 ケルディオ覚悟 みず かくとう 260 192 209 4181 647.1
16 オオニューラ かくとう どく 259 158 190 3643 903.0
17 コジョンド かくとう 258 127 163 3064 620.0
18 ザマゼンタ かくとう はがね 254 236 192 4329 889.0
19 ザマゼンタ_ゆうしゃ かくとう 254 236 192 4329 889.1
20 ウーラオス(れんげき) かくとう みず 254 177 225 4077 892.0
エスパー
Name type1 type2 ATK DEF HP CP_PL50 No
1 メガミュウツーY エスパー 426 229 235 7690 150.20
2 デオキシスA エスパー 414 46 137 2916 386.01
3 メガミュウツーX エスパー かくとう 412 222 235 7339 150.10
4 メガフーディン エスパー 367 207 146 5099 65.10
5 デオキシスN エスパー 345 115 137 3573 386.00
6 メガラティオス ドラゴン エスパー 335 241 190 5661 381.10
7 メガサーナイト エスパー フェアリー 326 229 169 5101 282.10
8 メガエルレイド エスパー かくとう 326 230 169 5112 475.10
9 フーパ(解放) エスパー あく 311 191 173 4530 720.10
10 ミュウツー エスパー 300 182 214 4724 150.00
11 メガメタグロス はがね エスパー 300 289 190 5552 376.10
12 メガラティアス ドラゴン エスパー 289 297 190 5428 380.10
13 フーディン エスパー 271 167 146 3456 65.00
14 アグノム エスパー 270 151 181 3629 482.00
15 ラティオス ドラゴン エスパー 268 212 190 4310 381.00
16 エーフィ エスパー 261 175 163 3583 196.00
17 フーパ(戒め) エスパー ゴースト 261 187 173 3797 720.00
18 カプ・テテフ エスパー フェアリー 259 208 172 3950 786.00
19 メタグロス はがね エスパー 257 228 190 4286 376.00
20 ソルガレオ エスパー はがね 255 191 264 4570 791.00
いわ
Name type1 type2 ATK DEF HP CP_PL50 No
1 メガディアンシー いわ フェアリー 342 235 137 4913 719.10
2 メガバンギラス いわ あく 309 276 225 6045 248.10
3 ラムパルド いわ 295 109 219 3728 409.00
4 メガプテラ いわ ひこう 292 210 190 4655 142.10
5 アーケオス いわ ひこう 292 139 181 3766 567.00
6 テラキオン いわ かくとう 260 192 209 4181 639.00
7 バサギリ むし いわ 253 174 172 3557 900.00
8 バンギラス いわ あく 251 207 225 4335 248.00
9 テツノイバラ いわ でんき 250 200 225 4250 991.00
10 ウツロイド いわ どく 249 210 240 4465 793.00
11 キラフロル いわ どく 246 177 195 3700 967.00
12 ドサイドン じめん いわ 241 190 251 4221 464.00
13 アルセウス(いわ) いわ 238 238 237 4510 493.14
14 ルガルガンたそがれ いわ 234 139 181 3054 745.20
15 ウインディH ほのお いわ 232 165 216 3556 59.10
16 ルガルガン昼 いわ 231 140 181 3027 745.00
17 ガチゴラス いわ ドラゴン 227 191 193 3537 697.00
18 ギガイアス いわ 226 201 198 3650 526.00
19 サイドン じめん いわ 222 171 233 3594 112.00
20 アーマルド いわ むし 222 174 181 3220 348.00
ゴースト
Name type1 type2 ATK DEF HP CP_PL50 No
1 メガゲンガー ゴースト どく 349 199 155 4902 94.10
2 ズガドーン ほのお ゴースト 315 148 142 3727 806.00
3 メガジュペッタ ゴースト 312 160 162 4063 354.10
4 ギルガルド剣 はがね ゴースト 291 97 155 2981 681.10
5 ハバタクカミ ゴースト フェアリー 280 235 146 4179 983.00
6 レイスポス ゴースト 273 147 205 3839 897.00
7 シャンデラ ゴースト ほのお 271 182 155 3695 609.00
8 ドラパルト ドラゴン ゴースト 266 170 204 3993 887.00
9 マーシャドー かくとう ゴースト 265 190 207 4217 802.00
10 ゲンガー ゴースト どく 261 149 155 3254 94.00
11 フーパ(戒め) エスパー ゴースト 261 187 173 3797 720.00
12 ゾロアークH ノーマル ゴースト 261 128 146 2957 571.10
13 ルナアーラ エスパー ゴースト 255 191 264 4570 792.00
14 サニゴーン ゴースト 253 182 155 3463 864.00
15 サーフゴー はがね ゴースト 252 190 202 3976 977.00
16 ポットデス ゴースト 248 189 155 3458 855.00
17 ソウブレイズ ほのお ゴースト 239 189 181 3586 1005.00
18 バクフーンH ほのお ゴースト 238 172 177 3385 157.10
19 アルセウス(ゴースト) ゴースト 238 238 237 4510 493.15
20 ダダリン ゴースト くさ 233 179 172 3335 781.00
ドラゴン
Name type1 type2 ATK DEF HP CP_PL50 No
1 メガレックウザ ドラゴン ひこう 389 216 233 6827 384.1
2 メガガブリアス ドラゴン じめん 339 222 239 6132 445.1
3 メガラティオス ドラゴン エスパー 335 241 190 5661 381.1
4 メガジュカイン くさ ドラゴン 320 186 172 4585 254.1
5 メガボーマンダ ドラゴン ひこう 310 251 216 5688 373.1
6 ブラックキュレム ドラゴン こおり 310 183 245 5206 646.1
7 ホワイトキュレム ドラゴン こおり 310 183 245 5206 646.2
8 メガデンリュウ でんき ドラゴン 294 203 207 4799 181.1
9 メガラティアス ドラゴン エスパー 289 297 190 5428 380.1
10 パルキアO みず ドラゴン 286 223 189 4683 484.1
11 レックウザ ドラゴン ひこう 284 170 213 4336 384.0
12 オノノクス ドラゴン 284 172 183 4062 612.0
13 パルキア みず ドラゴン 280 215 189 4512 484.0
14 ムゲンダイナ どく ドラゴン 278 192 268 5007 890.0
15 ボーマンダ ドラゴン ひこう 277 168 216 4239 373.0
16 ディアルガ はがね ドラゴン 275 211 205 4565 483.0
17 レシラム ドラゴン ほのお 275 211 205 4565 643.0
18 ゼクロム ドラゴン でんき 275 211 205 4565 644.0
19 メガリザードンX ほのお ドラゴン 273 213 186 4353 6.1
20 ディアルガO はがね ドラゴン 270 225 205 4624 483.1
はがね
Name type1 type2 ATK DEF HP CP_PL50 No
1 ザシアン_けんのおう フェアリー はがね 331 240 192 5613 888.2
2 カミツルギ くさ はがね 323 182 139 4156 798.0
3 メガルカリオ かくとう はがね 310 175 172 4325 448.1
4 メガメタグロス はがね エスパー 300 289 190 5552 376.1
5 ギルガルド剣 はがね ゴースト 291 97 155 2981 681.1
6 メガハッサム むし はがね 279 250 172 4621 212.1
7 ディアルガ はがね ドラゴン 275 211 205 4565 483.0
8 ディアルガO はがね ドラゴン 270 225 205 4624 483.1
9 メタグロス はがね エスパー 257 228 190 4286 376.0
10 ドリュウズ じめん はがね 255 129 242 3667 530.0
11 ソルガレオ エスパー はがね 255 191 264 4570 791.0
12 ザシアン フェアリー はがね 254 236 192 4329 888.0
13 ザマゼンタ かくとう はがね 254 236 192 4329 889.0
14 ゲノセクト むし はがね 252 199 174 3791 649.0
15 ゲノセクト水 むし はがね 252 199 174 3791 649.1
16 ゲノセクト電気 むし はがね 252 199 174 3791 649.2
17 ゲノセクト炎 むし はがね 252 199 174 3791 649.3
18 ゲノセクト氷 むし はがね 252 199 174 3791 649.4
19 サーフゴー はがね ゴースト 252 190 202 3976 977.0
20 ヒードラン ほのお はがね 251 213 209 4244 485.0
ひこう
Name type1 type2 ATK DEF HP CP_PL50 No
1 メガレックウザ ドラゴン ひこう 389 216 233 6827 384.10
2 メガリザードンY ほのお ひこう 319 212 186 5037 6.20
3 メガボーマンダ ドラゴン ひこう 310 251 216 5688 373.10
4 メガカイロス むし ひこう 305 231 163 4728 127.10
5 ボルトロス霊獣 でんき ひこう 295 161 188 4137 642.10
6 メガプテラ いわ ひこう 292 210 190 4655 142.10
7 アーケオス いわ ひこう 292 139 181 3766 567.00
8 ランドロス霊獣 じめん ひこう 289 179 205 4434 645.10
9 レックウザ ドラゴン ひこう 284 170 213 4336 384.00
10 ラブトロス化身 フェアリー ひこう 281 162 179 3873 905.00
11 メガピジョット ノーマル ひこう 280 175 195 4160 18.10
12 ボーマンダ ドラゴン ひこう 277 168 216 4239 373.00
13 トルネロス化身 ひこう 266 164 188 3782 641.00
14 ボルトロス化身 でんき ひこう 266 164 188 3782 642.00
15 カイリュー ドラゴン ひこう 263 198 209 4287 149.00
16 シェイミS くさ ひこう 261 166 225 4061 492.01
17 ランドロス化身 じめん ひこう 261 182 205 4057 645.00
18 サンダー でんき ひこう 253 185 207 3987 145.00
19 サンダーG かくとう ひこう 252 189 207 4012 145.10
20 ファイヤー ほのお ひこう 251 181 207 3917 146.00
メガポケモンのタイプの表
ポケモンGOでメガポケモンによるブーストを考える時、メガポケモンのタイプのリストがあったら便利かなと作成。
種族値は原作からの推定値です。
くさ
Name type1 type2 ATK DEF HP No
1 メガジュカイン くさ ドラゴン 320 186 172 254.1
2 メガフシギバナ くさ どく 241 246 190 3.1
3 メガユキノオー くさ こおり 240 191 207 460.1
ほのお
Name type1 type2 ATK DEF HP No
1 ゲンシグラードン じめん ほのお 364 276 225 383.1
2 メガバシャーモ ほのお かくとう 329 168 190 257.1
3 メガリザードンY ほのお ひこう 319 212 186 6.2
4 メガヘルガー あく ほのお 289 194 181 229.1
5 メガリザードンX ほのお ドラゴン 273 213 186 6.1
6 メガバクーダ ほのお じめん 253 183 172 323.1
みず
Name type1 type2 ATK DEF HP No
1 ゲンシカイオーガ みず 364 276 225 382.1
2 メガギャラドス みず あく 292 247 216 130.1
3 メガサメハダー みず あく 289 144 172 319.1
4 メガラグラージ みず じめん 283 218 225 260.1
5 メガカメックス みず 264 237 188 9.1
6 メガヤドラン みず エスパー 224 259 216 80.1
むし
Name type1 type2 ATK DEF HP No
1 メガヘラクロス むし かくとう 334 223 190 214.1
2 メガカイロス むし ひこう 305 231 163 127.1
3 メガスピアー むし どく 303 148 163 15.1
4 メガハッサム むし はがね 279 250 172 212.1
ノーマル
Name type1 type2 ATK DEF HP No
1 メガミミロップ ノーマル かくとう 282 214 163 428.1
2 メガピジョット ノーマル ひこう 280 175 195 18.1
3 メガガルーラ ノーマル 246 210 233 115.1
4 メガタブンネ ノーマル フェアリー 147 239 230 531.1
あく
Name type1 type2 ATK DEF HP No
1 メガアブソル あく 314 130 163 359.1
2 メガバンギラス いわ あく 309 276 225 248.1
3 メガギャラドス みず あく 292 247 216 130.1
4 メガヘルガー あく ほのお 289 194 181 229.1
5 メガサメハダー みず あく 289 144 172 319.1
6 メガヤミラミ あく ゴースト 151 216 137 302.1
どく
Name type1 type2 ATK DEF HP No
1 メガゲンガー ゴースト どく 349 199 155 94.1
2 メガスピアー むし どく 303 148 163 15.1
3 メガフシギバナ くさ どく 241 246 190 3.1
でんき
Name type1 type2 ATK DEF HP No
1 メガデンリュウ でんき ドラゴン 294 203 207 181.1
2 メガライボルト でんき 286 179 172 310.1
じめん
Name type1 type2 ATK DEF HP No
1 ゲンシグラードン じめん ほのお 364 276 225 383.1
2 メガガブリアス ドラゴン じめん 339 222 239 445.1
3 メガラグラージ みず じめん 283 218 225 260.1
4 メガバクーダ ほのお じめん 253 183 172 323.1
5 メガハガネール はがね じめん 212 327 181 208.1
こおり
Name type1 type2 ATK DEF HP No
1 メガオニゴーリ こおり 252 168 190 362.1
2 メガユキノオー くさ こおり 240 191 207 460.1
フェアリー
Name type1 type2 ATK DEF HP No
1 メガディアンシー いわ フェアリー 342 235 137 719.1
2 メガサーナイト エスパー フェアリー 326 229 169 282.1
3 メガチルタリス ドラゴン フェアリー 222 218 181 334.1
4 メガクチート はがね フェアリー 188 217 137 303.1
5 メガタブンネ ノーマル フェアリー 147 239 230 531.1
かくとう
Name type1 type2 ATK DEF HP No
1 メガミュウツーX エスパー かくとう 412 222 235 150.1
2 メガヘラクロス むし かくとう 334 223 190 214.1
3 メガバシャーモ ほのお かくとう 329 168 190 257.1
4 メガエルレイド エスパー かくとう 326 230 169 475.1
5 メガルカリオ かくとう はがね 310 175 172 448.1
6 メガミミロップ ノーマル かくとう 282 214 163 428.1
7 メガチャーレム かくとう エスパー 205 179 155 308.1
エスパー
Name type1 type2 ATK DEF HP No
1 メガミュウツーY エスパー 426 229 235 150.2
2 メガミュウツーX エスパー かくとう 412 222 235 150.1
3 メガフーディン エスパー 367 207 146 65.1
4 メガラティオス ドラゴン エスパー 335 241 190 381.1
5 メガサーナイト エスパー フェアリー 326 229 169 282.1
6 メガエルレイド エスパー かくとう 326 230 169 475.1
7 メガメタグロス はがね エスパー 300 289 190 376.1
8 メガラティアス ドラゴン エスパー 289 297 190 380.1
9 メガヤドラン みず エスパー 224 259 216 80.1
10 メガチャーレム かくとう エスパー 205 179 155 308.1
いわ
Name type1 type2 ATK DEF HP No
1 メガディアンシー いわ フェアリー 342 235 137 719.1
2 メガバンギラス いわ あく 309 276 225 248.1
3 メガプテラ いわ ひこう 292 210 190 142.1
ゴースト
Name type1 type2 ATK DEF HP No
1 メガゲンガー ゴースト どく 349 199 155 94.1
2 メガジュペッタ ゴースト 312 160 162 354.1
3 メガヤミラミ あく ゴースト 151 216 137 302.1
ドラゴン
Name type1 type2 ATK DEF HP No
1 メガレックウザ ドラゴン ひこう 389 216 233 384.1
2 メガガブリアス ドラゴン じめん 339 222 239 445.1
3 メガラティオス ドラゴン エスパー 335 241 190 381.1
4 メガジュカイン くさ ドラゴン 320 186 172 254.1
5 メガボーマンダ ドラゴン ひこう 310 251 216 373.1
6 メガデンリュウ でんき ドラゴン 294 203 207 181.1
7 メガラティアス ドラゴン エスパー 289 297 190 380.1
8 メガリザードンX ほのお ドラゴン 273 213 186 6.1
9 メガチルタリス ドラゴン フェアリー 222 218 181 334.1
はがね
Name type1 type2 ATK DEF HP No
1 メガルカリオ かくとう はがね 310 175 172 448.1
2 メガメタグロス はがね エスパー 300 289 190 376.1
3 メガハッサム むし はがね 279 250 172 212.1
4 メガボスゴドラ はがね 247 331 172 306.1
5 メガハガネール はがね じめん 212 327 181 208.1
6 メガクチート はがね フェアリー 188 217 137 303.1
ひこう
Name type1 type2 ATK DEF HP No
1 メガレックウザ ドラゴン ひこう 389 216 233 384.1
2 メガリザードンY ほのお ひこう 319 212 186 6.2
3 メガボーマンダ ドラゴン ひこう 310 251 216 373.1
4 メガカイロス むし ひこう 305 231 163 127.1
5 メガプテラ いわ ひこう 292 210 190 142.1
6 メガピジョット ノーマル ひこう 280 175 195 18.1
ポケモンレベル50まで考慮したリトルリーグCP500以下の順位
ポケモンレベル55までGameMasterに掲載されたので、レベル50まで考慮したリトルリーグ(CP500以下)の順位を各タイプで作成
当面レベルは50までなので50までで再計算
この中で良い技のやつが活躍するわけですな
rADH_500=CP500以下でのmax√(攻*防*HP)
すべて
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 ツボツボ むし いわ 17 396 85 883 50.0
2 ラッキー ノーマル 60 128 487 863 17.5
3 ドーミラー はがね エスパー 43 154 149 833 49.5
4 ソーナンス エスパー 60 106 382 821 21.5
5 コスモウム エスパー 54 242 125 814 27.5
6 ソーナノ エスパー 41 86 216 798 50.0
7 マリル みず フェアリー 37 93 172 771 50.0
8 トリデプス いわ はがね 94 286 155 737 13.5
9 ハピナス ノーマル 129 169 496 732 7.5
10 ギルガルド盾 はがね ゴースト 97 291 155 732 13.0
11 メレシー いわ フェアリー 95 285 137 725 14.0
12 ピンプク ノーマル 25 77 225 723 50.0
13 ドーブル ノーマル 40 83 146 717 50.0
14 チョボマキ むし 72 140 137 716 25.5
15 コフーライ むし 48 89 128 715 50.0
16 イワーク いわ じめん 85 232 111 711 19.0
17 トランセル むし 45 80 137 709 50.0
18 タテトプス いわ はがね 76 195 102 709 24.0
19 ノズパス いわ 82 215 102 707 21.0
20 ナマコブシ みず 97 224 146 706 15.0
21 ホーホー ノーマル ひこう 67 88 155 705 33.5
22 カラサリス むし 60 77 137 704 50.0
23 マユルド むし 60 77 137 704 50.0
24 キノココ くさ 74 110 155 703 26.0
25 トゲピー フェアリー 67 116 111 698 36.0
26 チルット ノーマル ひこう 76 132 128 696 25.5
27 ヨマワル ゴースト 70 162 85 696 30.0
28 ブラッキー あく 126 240 216 695 9.5
29 パチリス でんき 94 172 155 695 17.0
30 ミノムッチ むし 53 83 120 694 49.5
31 テッシード くさ はがね 82 155 127 694 22.0
32 レディバ むし ひこう 72 118 120 693 29.0
33 レドームシ むし エスパー 87 157 137 693 20.0
34 カジッチュ くさ ドラゴン 71 116 120 693 30.0
35 モンメン くさ フェアリー 71 111 120 691 30.5
36 パウワウ みず 85 121 163 690 21.5
37 ゴクリン どく 80 99 172 690 24.0
38 タブンネ ノーマル 114 163 230 689 12.0
39 ドヒドイデ どく みず 114 273 137 689 12.0
40 シズクモ みず むし 72 117 116 689 29.5
41 バルジーナ あく ひこう 129 205 242 688 9.0
42 ヒメンカ くさ 70 104 120 688 34.0
43 マリルリ みず フェアリー 112 152 225 687 12.5
44 クレセリア エスパー 152 258 260 687 7.0
45 スリープ エスパー 89 136 155 686 20.0
46 ドクケイル むし どく 98 162 155 685 16.5
47 ヤジロン じめん エスパー 77 124 120 685 27.0
48 ハネッコ くさ ひこう 67 94 111 684 42.0
49 コクーン むし どく 46 75 128 682 50.0
50 ジグザグマ ノーマル 58 80 116 682 50.0
51 ジグザグマG ノーマル あく 58 80 116 682 50.0
52 ラブカス みず 81 128 125 680 24.5
53 レジスチル はがね 143 285 190 680 8.0
54 カラカラ じめん 90 144 137 678 20.0
55 ベロリンガ ノーマル 108 137 207 675 14.0
56 ホルード ノーマル じめん 112 155 198 675 13.0
57 ムゲンダイナ_無限大max どく ドラゴン 250 505 452 675 2.5
58 ワタッコ くさ ひこう 118 183 181 674 12.0
59 メガタブンネ ノーマル フェアリー 147 239 230 674 8.0
60 アママイコ くさ 78 94 141 674 27.5
61 ママンボウ みず 138 131 338 673 9.0
62 ワンパチ でんき 80 90 153 673 26.5
63 レディアン むし ひこう 107 179 146 672 15.0
64 コアルヒー みず ひこう 84 96 158 672 24.0
65 リリーラ いわ くさ 105 150 165 671 15.5
66 ダイノーズ いわ はがね 135 275 155 671 9.5
67 アマカジ くさ 55 69 123 671 50.0
68 トロッゴン いわ ほのお 114 157 190 671 13.0
69 オニシズクモ みず むし 126 219 169 670 11.0
70 ポポッコ くさ ひこう 91 120 146 669 21.0
71 ミツハニー むし ひこう 59 83 102 669 50.0
72 メテノ(流星) いわ ひこう 116 194 155 669 13.0
73 ウールー ノーマル 76 97 123 669 29.5
74 ツチニン むし じめん 80 126 104 668 27.0
75 ピィ フェアリー 75 79 137 667 32.5
76 スコルピ どく むし 93 151 120 667 20.0
77 バルチャイ あく ひこう 105 139 172 667 16.0
78 ジガルデ完全 ドラゴン じめん 184 207 389 667 5.5
79 ハガネール はがね じめん 148 272 181 665 8.0
80 ハスボー みず くさ 71 77 120 665 41.0
81 タネボー くさ 71 77 120 665 41.0
82 タマンタ みず ひこう 105 179 128 665 16.0
83 ホルビー ノーマル 68 72 116 665 48.5
84 セキタンザン いわ ほのお 146 198 242 665 8.5
85 ホイーガ むし どく 100 173 120 664 18.0
86 サニーゴG ゴースト 116 182 155 664 13.5
87 デオキシスD エスパー 144 330 137 663 8.5
88 メノクラゲ みず どく 97 149 120 661 19.5
89 ウパー みず じめん 75 66 146 661 35.5
90 アサナン かくとう エスパー 78 107 102 661 30.5
91 プリン ノーマル フェアリー 80 41 251 659 29.0
92 トロピウス くさ ひこう 136 163 223 658 10.0
93 ビッパ ノーマル 80 73 153 658 29.0
94 マッギョ じめん でんき 144 171 240 658 9.0
95 タンドン いわ 73 91 102 658 39.0
96 マッギョG じめん はがね 144 171 240 658 9.0
97 ニドラン♀ どく 86 89 146 657 25.5
98 チコリータ くさ 92 122 128 657 22.0
99 デスマス ゴースト 95 141 116 656 21.0
100 ヤブクロン どく 96 122 137 656 20.5
くさ
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 キノココ くさ 74 110 155 703 26.0
2 テッシード くさ はがね 82 155 127 694 22.0
3 カジッチュ くさ ドラゴン 71 116 120 693 30.0
4 モンメン くさ フェアリー 71 111 120 691 30.5
5 ヒメンカ くさ 70 104 120 688 34.0
6 ハネッコ くさ ひこう 67 94 111 684 42.0
7 ワタッコ くさ ひこう 118 183 181 674 12.0
8 アママイコ くさ 78 94 141 674 27.5
9 リリーラ いわ くさ 105 150 165 671 15.5
10 アマカジ くさ 55 69 123 671 50.0
11 ポポッコ くさ ひこう 91 120 146 669 21.0
12 ハスボー みず くさ 71 77 120 665 41.0
13 タネボー くさ 71 77 120 665 41.0
14 トロピウス くさ ひこう 136 163 223 658 10.0
15 チコリータ くさ 92 122 128 657 22.0
16 ツタージャ くさ 88 107 128 655 24.5
17 クルマユ むし くさ 115 162 146 653 14.5
18 クルミル むし くさ 96 124 128 652 21.0
19 タマタマ くさ エスパー 107 125 155 650 17.0
20 タマゲタケ くさ どく 97 91 170 649 20.5
21 モクロー くさ ひこう 102 99 169 649 19.0
22 スボミー くさ どく 91 109 120 648 24.0
23 ベイリーフ くさ 122 155 155 644 13.5
24 ユレイドル いわ くさ 152 194 200 642 9.0
25 ジャノビー くさ 122 152 155 641 13.5
26 ナットレイ くさ はがね 158 223 179 640 8.5
27 ハスブレロ みず くさ 112 119 155 638 16.5
28 モロバレル くさ どく 155 139 249 633 9.0
29 ワタシラガ くさ 148 211 155 633 9.5
30 ミノマダム草 むし くさ 141 180 155 631 11.0
31 ジャローダ くさ 161 204 181 631 8.5
32 ハリマロン くさ 110 106 148 630 18.0
33 バケッチャ特大 ゴースト くさ 118 120 153 630 16.0
34 メガニウム くさ 168 202 190 626 8.0
35 ヤナップ くさ 104 94 137 626 21.0
36 ネマシュ くさ フェアリー 108 119 120 626 19.5
37 フクスロー くさ ひこう 142 139 186 625 11.0
38 ユキカブリ くさ こおり 115 105 155 624 17.0
39 シキジカ ノーマル くさ 115 100 155 624 17.5
40 ビリジオン くさ かくとう 192 229 209 624 6.5
ほのお
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 トロッゴン いわ ほのお 114 157 190 671 13.0
2 セキタンザン いわ ほのお 146 198 242 665 8.5
3 ロコン ほのお 96 109 116 637 23.0
4 コータス ほのお 151 203 172 635 9.5
5 ガラガラA ほのお ゴースト 144 186 155 631 10.5
6 マグカルゴ ほのお いわ 139 191 137 629 11.5
7 バオップ ほのお 104 94 137 626 21.0
8 ヒトモシ ゴースト ほのお 108 98 137 623 20.0
9 キュウコン ほのお 169 190 177 618 8.5
10 バクガメス ほのお ドラゴン 165 215 155 617 8.5
11 ポカブ ほのお 115 85 163 613 18.5
12 ビクティニ エスパー ほのお 210 210 225 610 6.0
13 フォッコ ほのお 116 102 120 604 19.0
14 ヤクデ ほのお むし 118 90 137 602 19.0
15 ドンメル ほのお じめん 119 79 155 601 18.5
16 アルセウス(ほのお) ほのお 238 238 237 601 5.0
17 ヒコザル ほのお 113 86 127 600 21.0
18 シシコ ほのお ノーマル 139 112 158 600 13.5
19 ヒトカゲ ほのお 116 93 118 598 20.5
20 ヒノアラシ ほのお 116 93 118 598 20.5
21 ファイアロー ほのお ひこう 176 155 186 597 9.0
22 ホウオウ ほのお ひこう 239 244 214 593 5.0
23 ヒノヤコマ ほのお ひこう 145 110 158 593 13.0
24 ガオガエン ほのお あく 214 175 216 590 6.5
25 リザード ほのお 158 126 151 587 11.5
26 マグマラシ ほのお 158 126 151 587 11.5
27 ガーディ ほのお 136 93 146 586 16.0
28 チャオブー ほのお かくとう 173 106 207 585 10.0
29 エンテイ ほのお 235 171 251 582 5.5
30 アチャモ ほのお 130 87 128 582 18.0
31 ロトム炎 でんき ほのお 204 219 137 582 7.5
32 ラビフット ほのお 170 125 163 582 10.5
33 マルヤクデ ほのお むし 220 158 225 582 6.5
34 ワカシャモ ほのお かくとう 163 115 155 580 11.5
35 ヒヒダルマD ほのお エスパー 243 202 233 580 5.5
36 モウカザル ほのお かくとう 158 105 162 579 12.5
37 ニャビー ほのお 128 79 128 579 19.0
38 ヒバニー ほのお 132 79 137 579 18.0
39 マグマッグ ほのお 118 71 120 578 22.0
40 テールナー ほのお 171 130 153 578 10.5
みず
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 マリル みず フェアリー 37 93 172 771 50.0
2 ナマコブシ みず 97 224 146 706 15.0
3 パウワウ みず 85 121 163 690 21.5
4 ドヒドイデ どく みず 114 273 137 689 12.0
5 シズクモ みず むし 72 117 116 689 29.5
6 マリルリ みず フェアリー 112 152 225 687 12.5
7 ラブカス みず 81 128 125 680 24.5
8 ママンボウ みず 138 131 338 673 9.0
9 コアルヒー みず ひこう 84 96 158 672 24.0
10 オニシズクモ みず むし 126 219 169 670 11.0
11 ハスボー みず くさ 71 77 120 665 41.0
12 タマンタ みず ひこう 105 179 128 665 16.0
13 メノクラゲ みず どく 97 149 120 661 19.5
14 ウパー みず じめん 75 66 146 661 35.5
15 カラナクシ みず 103 105 183 655 18.0
16 ゼニガメ みず 94 121 127 653 21.5
17 ジュゴン みず こおり 139 177 207 653 10.0
18 タマザラシ こおり みず 95 90 172 653 21.0
19 ケイコウオ みず 96 116 135 652 21.0
20 ヤドン みず エスパー 109 98 207 650 16.0
21 ラプラス みず こおり 165 174 277 648 7.5
22 カメテテ いわ みず 96 120 123 648 21.5
23 ランターン みず でんき 146 137 268 646 9.5
24 ヒドイデ どく みず 98 110 137 646 21.0
25 チョンチー みず でんき 106 97 181 645 18.0
26 サニーゴ みず いわ 118 156 146 645 14.5
27 マンタイン みず ひこう 148 226 163 642 9.0
28 ジーランス みず いわ 162 203 225 641 8.0
29 スイクン みず 180 235 225 640 6.5
30 コソクムシ むし みず 67 74 93 639 50.0
31 ハスブレロ みず くさ 112 119 155 638 16.5
32 プルリル みず ゴースト 115 134 146 638 16.0
33 ブルンゲル みず ゴースト 159 178 225 638 8.5
34 カメール みず 126 155 153 637 13.5
35 ナマズン みず じめん 151 141 242 635 9.5
36 ドジョッチ みず じめん 93 82 137 634 25.0
37 トドグラー こおり みず 137 132 207 634 11.5
38 ウデッポウ みず 108 117 137 634 18.5
39 ネオラント みず 142 170 170 632 10.5
40 ドククラゲ みず どく 166 209 190 631 8.0
むし
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 ツボツボ むし いわ 17 396 85 883 50.0
2 チョボマキ むし 72 140 137 716 25.5
3 コフーライ むし 48 89 128 715 50.0
4 トランセル むし 45 80 137 709 50.0
5 カラサリス むし 60 77 137 704 50.0
6 マユルド むし 60 77 137 704 50.0
7 ミノムッチ むし 53 83 120 694 49.5
8 レディバ むし ひこう 72 118 120 693 29.0
9 レドームシ むし エスパー 87 157 137 693 20.0
10 シズクモ みず むし 72 117 116 689 29.5
11 ドクケイル むし どく 98 162 155 685 16.5
12 コクーン むし どく 46 75 128 682 50.0
13 レディアン むし ひこう 107 179 146 672 15.0
14 オニシズクモ みず むし 126 219 169 670 11.0
15 ミツハニー むし ひこう 59 83 102 669 50.0
16 ツチニン むし じめん 80 126 104 668 27.0
17 スコルピ どく むし 93 151 120 667 20.0
18 ホイーガ むし どく 100 173 120 664 18.0
19 クルマユ むし くさ 115 162 146 653 14.5
20 クルミル むし くさ 96 124 128 652 21.0
21 コフキムシ むし 63 63 116 651 50.0
22 ミノマダム鋼 むし はがね 127 175 155 645 12.5
23 キャタピー むし 55 55 128 644 50.0
24 コンパン むし どく 100 100 155 644 20.0
25 フシデ むし どく 83 99 102 644 29.5
26 ケムッソ むし 75 59 128 643 43.0
27 クヌギダマ むし 108 122 137 639 18.0
28 コソクムシ むし みず 67 74 93 639 50.0
29 コロボーシ むし 45 74 114 638 50.0
30 イオルブ むし エスパー 156 240 155 634 9.0
31 ビークイン むし ひこう 149 190 172 633 9.5
32 フォレトス むし はがね 161 205 181 632 8.5
33 ミノマダム草 むし くさ 141 180 155 631 11.0
34 ミノマダム地 むし じめん 141 180 155 631 11.0
35 アメタマ むし みず 93 87 120 627 25.5
36 イシズマイ むし いわ 118 128 137 627 16.0
37 ビードル むし どく 63 50 120 626 49.5
38 バルビート むし 143 166 163 626 11.0
39 イルミーゼ むし 143 166 163 626 11.0
40 ユキハミ こおり むし 76 59 102 624 50.0
ノーマル
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 ラッキー ノーマル 60 128 487 863 17.5
2 ハピナス ノーマル 129 169 496 732 7.5
3 ピンプク ノーマル 25 77 225 723 50.0
4 ドーブル ノーマル 40 83 146 717 50.0
5 ホーホー ノーマル ひこう 67 88 155 705 33.5
6 チルット ノーマル ひこう 76 132 128 696 25.5
7 タブンネ ノーマル 114 163 230 689 12.0
8 ジグザグマ ノーマル 58 80 116 682 50.0
9 ジグザグマG ノーマル あく 58 80 116 682 50.0
10 ベロリンガ ノーマル 108 137 207 675 14.0
11 ホルード ノーマル じめん 112 155 198 675 13.0
12 メガタブンネ ノーマル フェアリー 147 239 230 674 8.0
13 ウールー ノーマル 76 97 123 669 29.5
14 ホルビー ノーマル 68 72 116 665 48.5
15 プリン ノーマル フェアリー 80 41 251 659 29.0
16 ビッパ ノーマル 80 73 153 658 29.0
17 ププリン ノーマル フェアリー 69 32 207 654 49.5
18 ホシガリス ノーマル 95 86 172 651 21.5
19 ゴンベ ノーマル 137 117 286 649 10.5
20 ノコッチ ノーマル 131 128 225 647 11.5
21 エネコ ノーマル 84 79 137 647 28.0
22 メタモン ノーマル 91 91 134 643 24.5
23 イーブイ ノーマル 104 114 146 643 19.0
24 ヨルノズク ノーマル ひこう 145 156 225 643 9.5
25 ベロベルト ノーマル 161 181 242 643 8.0
26 ミルタンク ノーマル 157 193 216 642 8.5
27 ラッタA あく ノーマル 135 154 181 638 11.5
28 ヨクバリス ノーマル 160 156 260 638 8.0
29 オタチ ノーマル 79 73 111 637 37.5
30 カビゴン ノーマル 190 169 330 635 6.0
31 ナマケロ ノーマル 104 92 155 633 20.0
32 ポッポ ノーマル ひこう 85 73 120 632 30.5
33 パッチール ノーマル 116 116 155 631 16.5
34 ヤレユータン ノーマル エスパー 168 192 207 630 8.0
35 チラーミィ ノーマル 98 80 146 628 23.5
36 バイウールー ノーマル 159 198 176 628 9.0
37 ルリリ ノーマル フェアリー 36 71 137 627 50.0
38 エネコロロ ノーマル 132 127 172 626 13.0
39 ヤヤコマ ノーマル ひこう 95 80 128 625 25.5
40 ポワルン ノーマル 139 139 172 624 12.0
あく
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 ブラッキー あく 126 240 216 695 9.5
2 バルジーナ あく ひこう 129 205 242 688 9.0
3 ジグザグマG ノーマル あく 58 80 116 682 50.0
4 バルチャイ あく ひこう 105 139 172 667 16.0
5 クスネ あく 85 82 120 640 29.0
6 ラッタA あく ノーマル 135 154 181 638 11.5
7 マーイーカ あく エスパー 98 95 142 638 22.0
8 ズルズキン あく かくとう 163 222 163 628 8.5
9 メガヤミラミ あく ゴースト 151 216 137 626 10.0
10 タチフサグマ あく ノーマル 180 194 212 620 7.5
11 マッスグマG ノーマル あく 142 128 186 618 11.5
12 アクジキング あく ドラゴン 188 99 440 618 7.0
13 ベトベトンA どく あく 190 172 233 612 7.0
14 ニャースA あく 99 78 120 611 25.0
15 ズルッグ あく かくとう 132 132 137 610 14.5
16 ドラピオン どく あく 180 202 172 609 8.0
17 チョロネコ あく 98 73 121 609 26.5
18 モノズ あく ドラゴン 116 93 141 609 18.5
19 スカンプー どく あく 121 90 160 608 17.5
20 カラマネロ あく エスパー 177 165 200 606 8.0
21 ベトベターA どく あく 135 90 190 603 14.0
22 ヤミラミ あく ゴースト 141 136 137 603 13.0
23 ジヘッド あく ドラゴン 159 135 176 602 10.5
24 ベロバー あく フェアリー 103 69 128 602 25.0
25 フォクスライ あく 172 164 172 601 9.0
26 アルセウス(あく) あく 238 238 237 601 5.0
27 ミカルゲ ゴースト あく 169 199 137 600 9.5
28 ペルシアンA あく 158 136 163 597 11.0
29 ポチエナ あく 96 61 111 596 30.0
30 スカタンク どく あく 184 132 230 595 8.0
31 コノハナ くさ あく 134 78 172 591 16.0
32 ギモー あく フェアリー 145 102 163 591 13.5
33 ガオガエン ほのお あく 214 175 216 590 6.5
34 グラエナ あく 171 132 172 589 10.0
35 コラッタA あく ノーマル 103 70 102 587 27.0
36 ザルード あく くさ 242 215 233 586 5.0
37 バンギラス いわ あく 251 207 225 577 5.0
38 コマタナ あく はがね 154 114 128 575 13.5
39 イベルタル あく ひこう 250 185 246 574 5.0
40 ワルビアル じめん あく 229 158 216 571 6.5
どく
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 ゴクリン どく 80 99 172 690 24.0
2 ドヒドイデ どく みず 114 273 137 689 12.0
3 ドクケイル むし どく 98 162 155 685 16.5
4 コクーン むし どく 46 75 128 682 50.0
5 ムゲンダイナ_無限大max どく ドラゴン 250 505 452 675 2.5
6 スコルピ どく むし 93 151 120 667 20.0
7 ホイーガ むし どく 100 173 120 664 18.0
8 メノクラゲ みず どく 97 149 120 661 19.5
9 ニドラン♀ どく 86 89 146 657 25.5
10 ヤブクロン どく 96 122 137 656 20.5
11 マルノーム どく 140 159 225 651 10.0
12 タマゲタケ くさ どく 97 91 170 649 20.5
13 スボミー くさ どく 91 109 120 648 24.0
14 ヒドイデ どく みず 98 110 137 646 21.0
15 コンパン むし どく 100 100 155 644 20.0
16 フシデ むし どく 83 99 102 644 29.5
17 ニドリーナ どく 117 120 172 640 15.0
18 ズバット どく ひこう 83 73 120 636 32.0
19 モロバレル くさ どく 155 139 249 633 9.0
20 ドククラゲ みず どく 166 209 190 631 8.0
21 クズモー どく みず 109 109 137 628 19.0
22 ビードル むし どく 63 50 120 626 49.5
23 ドガース どく 119 141 120 623 16.5
24 フシギダネ くさ どく 118 111 128 612 18.0
25 ベトベトン どく 190 172 233 612 7.0
26 ベトベトンA どく あく 190 172 233 612 7.0
27 ベベノム どく 145 133 167 610 12.0
28 ニドクイン どく じめん 180 173 207 609 8.0
29 マタドガス どく 174 197 163 609 8.5
30 マタドガスG どく フェアリー 174 197 163 609 8.5
31 ドラピオン どく あく 180 202 172 609 8.0
32 ドラミドロ どく ドラゴン 177 207 163 609 8.0
33 スカンプー どく あく 121 90 160 608 17.5
34 ゴルバット どく ひこう 161 150 181 607 9.5
35 ヤドランG どく エスパー 182 156 216 605 8.0
36 フシギソウ くさ どく 151 143 155 604 11.5
37 アーボ どく 110 97 111 604 21.5
38 ニドラン♂ どく 105 76 130 604 23.5
39 エレズン でんき どく 97 65 120 604 28.0
40 ニドリーノ どく 137 111 156 603 14.0
でんき
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 パチリス でんき 94 172 155 695 17.0
2 ワンパチ でんき 80 90 153 673 26.5
3 マッギョ じめん でんき 144 171 240 658 9.0
4 ランターン みず でんき 146 137 268 646 9.5
5 チョンチー みず でんき 106 97 181 645 18.0
6 バチュル むし でんき 110 98 137 620 19.5
7 ビリリダマ でんき 109 111 120 619 20.0
8 デンヂムシ むし でんき 145 161 149 615 11.5
9 マイナン でんき 147 150 155 614 11.5
10 メリープ でんき 114 79 146 606 20.0
11 エレズン でんき どく 97 65 120 604 28.0
12 ピカチュウ でんき 112 96 111 602 21.0
13 イシツブテA いわ でんき 132 132 120 601 15.0
14 パッチルドン でんき こおり 190 166 207 601 7.5
15 アルセウス(でんき) でんき 238 238 237 601 5.0
16 ゴローンA いわ でんき 164 164 146 599 10.0
17 モココ でんき 145 109 172 599 13.0
18 マルマイン でんき 173 173 155 595 9.0
19 シビシラス でんき 105 78 111 595 24.5
20 シビビール でんき 156 130 163 595 11.5
21 パッチラゴン でんき ドラゴン 195 165 207 595 7.5
22 デデンネ でんき フェアリー 164 134 167 594 10.5
23 ゴローニャA いわ でんき 211 198 190 591 6.5
24 エリキテル でんき ノーマル 115 78 127 591 21.5
25 ピチュー でんき 77 53 85 589 50.0
26 エレキッド でんき 135 101 128 585 16.0
27 エモンガ でんき ひこう 158 127 146 584 12.0
28 デンリュウ でんき 211 169 207 583 7.0
29 ロトム炎 でんき ほのお 204 219 137 582 7.5
30 ロトム水 でんき みず 204 219 137 582 7.5
31 ロトム氷 でんき こおり 204 219 137 582 7.5
32 ロトム飛 でんき ひこう 204 219 137 582 7.5
33 ロトム草 でんき くさ 204 219 137 582 7.5
34 プラスル でんき 167 129 155 581 11.0
35 ラクライ でんき 123 78 120 579 20.5
36 バチンウニ でんき 176 161 134 579 10.0
37 コリンク でんき 117 64 128 578 22.5
38 シママ でんき 118 64 128 577 22.5
39 オドリドリ \n (ぱちぱち) でんき ひこう 196 145 181 575 8.0
40 トゲデマル でんき はがね 190 145 163 574 9.0
じめん
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 イワーク いわ じめん 85 232 111 711 19.0
2 ヤジロン じめん エスパー 77 124 120 685 27.0
3 カラカラ じめん 90 144 137 678 20.0
4 ホルード ノーマル じめん 112 155 198 675 13.0
5 ツチニン むし じめん 80 126 104 668 27.0
6 ジガルデ完全 ドラゴン じめん 184 207 389 667 5.5
7 ハガネール はがね じめん 148 272 181 665 8.0
8 ウパー みず じめん 75 66 146 661 35.5
9 マッギョ じめん でんき 144 171 240 658 9.0
10 マッギョG じめん はがね 144 171 240 658 9.0
11 デスマスG じめん ゴースト 95 141 116 656 21.0
12 ゴマゾウ じめん 107 98 207 654 16.5
13 ネンドール じめん エスパー 140 229 155 651 10.0
14 スナヘビ じめん 103 123 141 647 18.5
15 グライガー じめん ひこう 143 184 163 636 10.5
16 ナマズン みず じめん 151 141 242 635 9.5
17 ドジョッチ みず じめん 93 82 137 634 25.0
18 ガラガラ じめん 144 186 155 631 10.5
19 ミノマダム地 むし じめん 141 180 155 631 11.0
20 ヒポポタス じめん 124 118 169 630 14.5
21 デスバーン じめん ゴースト 163 237 151 628 8.5
22 ウリムー こおり じめん 90 69 137 627 27.5
23 ヌオー みず じめん 152 143 216 624 10.0
24 スナバァ ゴースト じめん 120 118 146 624 16.0
25 サイホーン じめん いわ 140 127 190 621 12.0
26 メガハガネール はがね じめん 212 327 181 621 5.5
27 ガマガル みず じめん 128 109 181 620 14.5
28 トリトドン みず じめん 169 143 244 619 8.5
29 ジガルデ50% ドラゴン じめん 203 232 239 619 6.0
30 グライオン じめん ひこう 185 222 181 613 7.0
31 シロデスナ ゴースト じめん 178 178 198 613 8.0
32 サンド じめん 126 120 137 610 16.0
33 ニドクイン どく じめん 180 173 207 609 8.0
34 ヨーギラス いわ じめん 115 93 137 609 19.0
35 カバルドン じめん 201 191 239 609 6.5
36 サナギラス いわ じめん 155 133 172 604 11.0
37 ガマゲロゲ みず じめん 188 150 233 604 7.5
38 ヌマクロー みず じめん 156 133 172 602 11.0
39 ドダイトス くさ じめん 202 188 216 602 6.5
40 イシツブテ いわ じめん 132 132 120 601 15.0
こおり
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 ジュゴン みず こおり 139 177 207 653 10.0
2 タマザラシ こおり みず 95 90 172 653 21.0
3 ラプラス みず こおり 165 174 277 648 7.5
4 レジアイス こおり 179 309 190 646 6.5
5 ユキワラシ こおり 95 95 137 642 23.0
6 コオリッポ_アイス こおり 148 195 181 641 9.5
7 コオリッポ_ナイス こおり 148 195 181 641 9.5
8 ロコンA こおり 96 109 116 637 23.0
9 トドグラー こおり みず 137 132 207 634 11.5
10 アマルス いわ こおり 124 109 184 629 14.5
11 カチコール こおり 117 120 146 628 16.0
12 ウリムー こおり じめん 90 69 137 627 27.5
13 ウオチルドン みず こおり 171 185 207 625 8.0
14 フリーザー こおり ひこう 192 236 207 624 6.5
15 ユキカブリ くさ こおり 115 105 155 624 17.0
16 クレベース こおり 196 240 216 624 6.0
17 ユキハミ こおり むし 76 59 102 624 50.0
18 トドゼルガ こおり みず 182 176 242 621 7.0
19 アマルルガ いわ こおり 186 163 265 621 7.0
20 サンドA こおり はがね 125 129 137 616 15.5
21 キュウコンA こおり フェアリー 170 193 177 616 8.5
22 オニゴーリ こおり 162 162 190 615 9.0
23 サンドパンA こおり はがね 177 195 181 614 8.0
24 フリージオ こおり 190 218 190 614 7.0
25 パルシェン みず こおり 186 256 137 606 7.5
26 ユキノオー くさ こおり 178 158 207 605 8.0
27 パッチルドン でんき こおり 190 166 207 601 7.5
28 アルセウス(こおり) こおり 238 238 237 601 5.0
29 バニプッチ こおり 118 106 113 600 19.5
30 イノムー こおり じめん 181 138 225 599 8.0
31 ユキメノコ こおり ゴースト 171 150 172 597 9.5
32 バニリッチ こおり 151 138 139 595 12.0
33 デリバード こおり ひこう 128 90 128 586 18.0
34 ロトム氷 でんき こおり 204 219 137 582 7.5
35 クマシュン こおり 128 74 146 582 18.5
36 バリコオル こおり エスパー 212 179 190 581 7.0
37 キュレム ドラゴン こおり 246 170 245 577 5.5
38 バリヤードG こおり エスパー 183 169 137 576 9.5
39 ダルマッカG こおり 153 86 172 576 13.5
40 バイバニラ こおり 218 184 174 573 7.0
フェアリー
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 マリル みず フェアリー 37 93 172 771 50.0
2 メレシー いわ フェアリー 95 285 137 725 14.0
3 トゲピー フェアリー 67 116 111 698 36.0
4 モンメン くさ フェアリー 71 111 120 691 30.5
5 マリルリ みず フェアリー 112 152 225 687 12.5
6 メガタブンネ ノーマル フェアリー 147 239 230 674 8.0
7 ピィ フェアリー 75 79 137 667 32.5
8 プリン ノーマル フェアリー 80 41 251 659 29.0
9 ププリン ノーマル フェアリー 69 32 207 654 49.5
10 シュシュプ フェアリー 110 113 186 651 16.0
11 ピッピ フェアリー 107 108 172 646 17.5
12 ペロッパフ フェアリー 109 119 158 645 17.0
13 マホミル フェアリー 90 97 128 644 25.0
14 トゲチック フェアリー ひこう 139 181 146 630 11.5
15 フラベベ フェアリー 108 120 127 630 19.0
16 ルリリ ノーマル フェアリー 36 71 137 627 50.0
17 ネマシュ くさ フェアリー 108 119 120 626 19.5
18 フラエッテ フェアリー 136 151 144 619 12.5
19 プクリン ノーマル フェアリー 156 90 295 617 10.0
20 キュウコンA こおり フェアリー 170 193 177 616 8.5
21 ラルトス エスパー フェアリー 79 59 99 616 47.0
22 カプ・レヒレ みず フェアリー 189 254 172 616 7.0
23 ピクシー フェアリー 178 162 216 612 8.0
24 マシェード くさ フェアリー 154 168 155 612 10.5
25 キュワワー フェアリー 165 215 139 612 9.0
26 フレフワン フェアリー 173 150 226 611 8.5
27 ペロリーム フェアリー 168 163 193 611 9.0
28 ディアンシー いわ フェアリー 190 285 137 610 7.0
29 マタドガスG どく フェアリー 174 197 163 609 8.5
30 クレッフィ はがね フェアリー 160 179 149 609 10.0
31 エルフーン くさ フェアリー 164 176 155 606 9.5
32 ニンフィア フェアリー 203 205 216 606 6.5
33 フラージェス フェアリー 212 244 186 603 6.0
34 ベロバー あく フェアリー 103 69 128 602 25.0
35 アルセウス(フェアリー) フェアリー 238 238 237 601 5.0
36 ミミッキュ ゴースト フェアリー 177 199 146 599 8.5
37 アブリー むし フェアリー 110 81 120 597 22.5
38 マネネ エスパー フェアリー 125 142 85 594 18.0
39 デデンネ でんき フェアリー 164 134 167 594 10.5
40 キルリア エスパー フェアリー 117 90 116 593 20.5
かくとう
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 アサナン かくとう エスパー 78 107 102 661 30.5
2 バルキー かくとう 64 64 111 645 50.0
3 チャーレム かくとう エスパー 121 152 155 642 14.0
4 ナゲキ かくとう 172 160 260 629 7.5
5 ズルズキン あく かくとう 163 222 163 628 8.5
6 コバルオン はがね かくとう 192 229 209 624 6.5
7 ビリジオン くさ かくとう 192 229 209 624 6.5
8 ジャランゴ ドラゴン かくとう 145 162 146 616 11.5
9 ニョロボン みず かくとう 182 184 207 615 7.5
10 マクノシタ かくとう 99 54 176 615 25.0
11 ズルッグ あく かくとう 132 132 137 610 14.5
12 タタッコ かくとう 121 103 137 607 17.5
13 ブリガロン くさ かくとう 201 204 204 604 6.5
14 カポエラー かくとう 173 207 137 601 9.0
15 ヌイコグマ ノーマル かくとう 136 95 172 601 14.5
16 アルセウス(かくとう) かくとう 238 238 237 601 5.0
17 ドッコラー かくとう 134 87 181 599 15.0
18 ヤンチャム かくとう 145 107 167 598 13.0
19 グレッグル どく かくとう 116 76 134 593 21.0
20 ジャラランガ ドラゴン かくとう 222 240 181 593 6.0
21 ドテッコツ かくとう 180 134 198 590 9.0
22 ワンリキー かくとう 137 82 172 589 15.0
23 ザマゼンタ_たてのおう かくとう はがね 249 292 192 589 5.0
24 ゴーリキー かくとう 177 125 190 586 9.5
25 ハリテヤマ かくとう 209 114 302 586 7.0
26 チャオブー ほのお かくとう 173 106 207 585 10.0
27 ルチャブル かくとう ひこう 195 153 186 585 8.0
28 タイレーツ かくとう 193 170 163 582 8.0
29 エビワラー かくとう 193 197 137 580 8.0
30 ワカシャモ ほのお かくとう 163 115 155 580 11.5
31 マッシブーン むし かくとう 236 197 216 580 5.5
32 モウカザル ほのお かくとう 158 105 162 579 12.5
33 ナゲツケサル かくとう 222 160 225 579 6.5
34 キテルグマ ノーマル かくとう 226 141 260 575 6.0
35 オトスパス かくとう 209 162 190 575 7.0
36 リオル かくとう 127 78 120 574 20.0
37 ザマゼンタ_ゆうしゃ かくとう 254 236 192 574 5.0
38 マケンカニ かくとう 150 104 132 572 14.0
39 メガチャーレム かくとう エスパー 205 179 155 571 7.5
40 ダクマ かくとう 170 112 155 570 11.5
エスパー
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 ドーミラー はがね エスパー 43 154 149 833 49.5
2 ソーナンス エスパー 60 106 382 821 21.5
3 コスモウム エスパー 54 242 125 814 27.5
4 ソーナノ エスパー 41 86 216 798 50.0
5 レドームシ むし エスパー 87 157 137 693 20.0
6 クレセリア エスパー 152 258 260 687 7.0
7 スリープ エスパー 89 136 155 686 20.0
8 ヤジロン じめん エスパー 77 124 120 685 27.0
9 デオキシスD エスパー 144 330 137 663 8.5
10 アサナン かくとう エスパー 78 107 102 661 30.5
11 ユクシー エスパー 156 270 181 654 7.5
12 ダンバル はがね エスパー 96 132 120 652 21.0
13 ルギア エスパー ひこう 193 310 235 651 5.5
14 ネンドール じめん エスパー 140 229 155 651 10.0
15 ヤドン みず エスパー 109 98 207 650 16.0
16 スリーパー エスパー 144 193 198 650 9.5
17 タマタマ くさ エスパー 107 125 155 650 17.0
18 ヤドンG エスパー 109 98 207 650 16.0
19 ミュウツーアーマード エスパー 182 278 214 644 6.0
20 チャーレム かくとう エスパー 121 152 155 642 14.0
21 ゴチム エスパー 98 112 128 641 21.5
22 コスモッグ エスパー 54 57 125 641 50.0
23 マーイーカ あく エスパー 98 95 142 638 22.0
24 ムンナ エスパー 111 92 183 636 17.5
25 メタング はがね エスパー 138 176 155 634 11.5
26 イオルブ むし エスパー 156 240 155 634 9.0
27 ヤレユータン ノーマル エスパー 168 192 207 630 8.0
28 ドータクン はがね エスパー 161 213 167 627 8.5
29 ミブリム エスパー 98 93 123 626 23.5
30 コロモリ エスパー ひこう 107 85 163 625 19.5
31 ニャスパー エスパー 120 114 158 625 16.0
32 ゴチミル エスパー 137 153 155 623 12.0
33 バネブー エスパー 125 122 155 621 15.0
34 ヤドラン みず エスパー 177 180 216 619 7.5
35 ヤドキング みず エスパー 177 180 216 619 7.5
36 ムシャーナ エスパー 183 166 253 618 7.0
37 ブーピッグ エスパー 171 188 190 617 8.0
38 ラルトス エスパー フェアリー 79 59 99 616 47.0
39 ゴチルゼル エスパー 176 205 172 615 8.0
40 ニャオニクス♂ エスパー 166 167 179 611 9.0
いわ
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 ツボツボ むし いわ 17 396 85 883 50.0
2 トリデプス いわ はがね 94 286 155 737 13.5
3 メレシー いわ フェアリー 95 285 137 725 14.0
4 イワーク いわ じめん 85 232 111 711 19.0
5 タテトプス いわ はがね 76 195 102 709 24.0
6 ノズパス いわ 82 215 102 707 21.0
7 リリーラ いわ くさ 105 150 165 671 15.5
8 ダイノーズ いわ はがね 135 275 155 671 9.5
9 トロッゴン いわ ほのお 114 157 190 671 13.0
10 メテノ(流星) いわ ひこう 116 194 155 669 13.0
11 セキタンザン いわ ほのお 146 198 242 665 8.5
12 タンドン いわ 73 91 102 658 39.0
13 カメテテ いわ みず 96 120 123 648 21.5
14 レジロック いわ 179 309 190 646 6.5
15 サニーゴ みず いわ 118 156 146 645 14.5
16 ユレイドル いわ くさ 152 194 200 642 9.0
17 ジーランス みず いわ 162 203 225 641 8.0
18 マグカルゴ ほのお いわ 139 191 137 629 11.5
19 アマルス いわ こおり 124 109 184 629 14.5
20 ココドラ はがね いわ 121 141 137 628 15.0
21 イシズマイ むし いわ 118 128 137 627 16.0
22 ウソハチ いわ 124 133 137 622 15.0
23 サイホーン じめん いわ 140 127 190 621 12.0
24 コドラ はがね いわ 158 198 155 621 9.5
25 アマルルガ いわ こおり 186 163 265 621 7.0
26 プロトーガ みず いわ 134 146 144 619 13.0
27 ダンゴロ いわ 121 110 146 616 16.5
28 ボスゴドラ はがね いわ 198 257 172 613 6.5
29 ウソッキー いわ 167 176 172 611 9.0
30 ディアンシー いわ フェアリー 190 285 137 610 7.0
31 ヨーギラス いわ じめん 115 93 137 609 19.0
32 サナギラス いわ じめん 155 133 172 604 11.0
33 ツンデツンデ いわ はがね 213 298 156 604 6.0
34 ルナトーン いわ エスパー 178 153 207 603 8.5
35 ソルロック いわ エスパー 178 153 207 603 8.5
36 イシツブテ いわ じめん 132 132 120 601 15.0
37 イシツブテA いわ でんき 132 132 120 601 15.0
38 イワパレス むし いわ 188 200 172 601 7.5
39 アルセウス(いわ) いわ 238 238 237 601 5.0
40 ゴローン いわ じめん 164 164 146 599 10.0
ゴースト
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 ギルガルド盾 はがね ゴースト 97 291 155 732 13.0
2 ヨマワル ゴースト 70 162 85 696 30.0
3 サニーゴG ゴースト 116 182 155 664 13.5
4 デスマス ゴースト 95 141 116 656 21.0
5 デスマスG じめん ゴースト 95 141 116 656 21.0
6 サマヨール ゴースト 124 234 120 652 12.5
7 ギラティナA ゴースト ドラゴン 187 225 284 646 6.0
8 プルリル みず ゴースト 115 134 146 638 16.0
9 ブルンゲル みず ゴースト 159 178 225 638 8.5
10 ガラガラA ほのお ゴースト 144 186 155 631 10.5
11 バケッチャ特大 ゴースト くさ 118 120 153 630 16.0
12 デスカーン ゴースト 163 237 151 628 8.5
13 デスバーン じめん ゴースト 163 237 151 628 8.5
14 フワンテ ゴースト ひこう 117 80 207 627 16.5
15 メガヤミラミ あく ゴースト 151 216 137 626 10.0
16 バケッチャ大 ゴースト くさ 120 122 144 624 16.0
17 スナバァ ゴースト じめん 120 118 146 624 16.0
18 ヒトモシ ゴースト ほのお 108 98 137 623 20.0
19 バケッチャ ゴースト くさ 121 123 135 618 16.0
20 パンプジン特大 ゴースト くさ 182 200 198 617 7.5
21 パンプジン大 ゴースト くさ 179 206 181 614 7.5
22 バケッチャ小 ゴースト くさ 122 124 127 613 16.5
23 パンプジン ゴースト くさ 175 213 163 613 8.0
24 シロデスナ ゴースト じめん 178 178 198 613 8.0
25 パンプジン小 ゴースト くさ 171 219 146 612 8.5
26 ヒトツキ はがね ゴースト 135 139 128 607 14.0
27 フワライド ゴースト ひこう 180 102 312 605 8.0
28 ヨノワール ゴースト 180 254 128 604 8.0
29 ヤミラミ あく ゴースト 141 136 137 603 13.0
30 ギラティナO ゴースト ドラゴン 225 187 284 603 5.5
31 ゴビット じめん ゴースト 127 92 153 601 16.5
32 アルセウス(ゴースト) ゴースト 238 238 237 601 5.0
33 ミカルゲ ゴースト あく 169 199 137 600 9.5
34 ミミッキュ ゴースト フェアリー 177 199 146 599 8.5
35 ユキメノコ こおり ゴースト 171 150 172 597 9.5
36 ボクレー ゴースト くさ 125 103 125 597 17.5
37 ニダンギル はがね ゴースト 188 206 153 596 8.0
38 ムウマ ゴースト 167 154 155 595 10.0
39 オーロット ゴースト くさ 201 154 198 584 7.5
40 ジュナイパー くさ ゴースト 210 179 186 584 7.0
ドラゴン
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 カジッチュ くさ ドラゴン 71 116 120 693 30.0
2 ムゲンダイナ_無限大max どく ドラゴン 250 505 452 675 2.5
3 ジガルデ完全 ドラゴン じめん 184 207 389 667 5.5
4 チルタリス ドラゴン ひこう 141 201 181 649 9.5
5 ギラティナA ゴースト ドラゴン 187 225 284 646 6.0
6 ヌメラ ドラゴン 101 112 128 637 21.0
7 オンバット ひこう ドラゴン 83 73 120 636 32.0
8 ジャラコ ドラゴン 102 108 128 632 21.0
9 ジガルデ50% ドラゴン じめん 203 232 239 619 6.0
10 アクジキング あく ドラゴン 188 99 440 618 7.0
11 ヌメイル ドラゴン 159 176 169 617 9.5
12 バクガメス ほのお ドラゴン 165 215 155 617 8.5
13 ウオノラゴン みず ドラゴン 175 185 207 617 8.0
14 ジャランゴ ドラゴン かくとう 145 162 146 616 11.5
15 タルップル くさ ドラゴン 178 146 242 613 8.0
16 モノズ あく ドラゴン 116 93 141 609 18.5
17 ドラミドロ どく ドラゴン 177 207 163 609 8.0
18 ギラティナO ゴースト ドラゴン 225 187 284 603 5.5
19 ジヘッド あく ドラゴン 159 135 176 602 10.5
20 ヌメルゴン ドラゴン 220 242 207 602 5.5
21 アルセウス(ドラゴン) ドラゴン 238 238 237 601 5.0
22 キングドラ みず ドラゴン 194 194 181 597 7.5
23 フカマル ドラゴン じめん 124 84 151 596 18.0
24 パッチラゴン でんき ドラゴン 195 165 207 595 7.5
25 コモルー ドラゴン 172 155 163 594 9.5
26 ミニリュウ ドラゴン 119 91 121 593 19.5
27 ラティアス ドラゴン エスパー 228 246 190 593 5.5
28 ジャラランガ ドラゴン かくとう 222 240 181 593 6.0
29 ビブラーバ じめん ドラゴン 134 99 137 591 16.0
30 オンバーン ひこう ドラゴン 205 175 198 591 7.0
31 ハクリュー ドラゴン 163 135 156 588 11.0
32 チゴラス いわ ドラゴン 158 123 151 585 11.5
33 メガチルタリス ドラゴン フェアリー 222 218 181 583 6.0
34 タツベイ ドラゴン 134 93 128 581 17.0
35 フライゴン じめん ドラゴン 205 168 190 580 7.5
36 ガバイト ドラゴン じめん 172 125 169 580 10.0
37 ドロンチ ドラゴン ゴースト 163 105 169 579 11.5
38 クリムガン ドラゴン 213 170 184 577 7.0
39 キュレム ドラゴン こおり 246 170 245 577 5.5
40 ガブリアス ドラゴン じめん 261 193 239 575 5.0
はがね
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 ドーミラー はがね エスパー 43 154 149 833 49.5
2 トリデプス いわ はがね 94 286 155 737 13.5
3 ギルガルド盾 はがね ゴースト 97 291 155 732 13.0
4 タテトプス いわ はがね 76 195 102 709 24.0
5 テッシード くさ はがね 82 155 127 694 22.0
6 レジスチル はがね 143 285 190 680 8.0
7 ダイノーズ いわ はがね 135 275 155 671 9.5
8 ハガネール はがね じめん 148 272 181 665 8.0
9 マッギョG じめん はがね 144 171 240 658 9.0
10 ダンバル はがね エスパー 96 132 120 652 21.0
11 ミノマダム鋼 むし はがね 127 175 155 645 12.5
12 ギアル はがね 98 121 120 643 21.0
13 エアームド はがね ひこう 148 226 163 642 9.0
14 ナットレイ くさ はがね 158 223 179 640 8.5
15 アーマーガア ひこう はがね 163 192 221 640 8.0
16 メタング はがね エスパー 138 176 155 634 11.5
17 フォレトス むし はがね 161 205 181 632 8.5
18 ココドラ はがね いわ 121 141 137 628 15.0
19 ドータクン はがね エスパー 161 213 167 627 8.5
20 コバルオン はがね かくとう 192 229 209 624 6.5
21 メガハガネール はがね じめん 212 327 181 621 5.5
22 コドラ はがね いわ 158 198 155 621 9.5
23 ギギアル はがね 150 174 155 620 10.5
24 サンドA こおり はがね 125 129 137 616 15.5
25 サンドパンA こおり はがね 177 195 181 614 8.0
26 ボスゴドラ はがね いわ 198 257 172 613 6.5
27 ジラーチ はがね エスパー 210 210 225 610 6.0
28 クレッフィ はがね フェアリー 160 179 149 609 10.0
29 ヒトツキ はがね ゴースト 135 139 128 607 14.0
30 メルタン はがね 118 99 130 607 18.5
31 ニャースG はがね 115 92 137 607 19.5
32 ツンデツンデ いわ はがね 213 298 156 604 6.0
33 メルメタル はがね 226 190 264 601 5.5
34 アルセウス(はがね) はがね 238 238 237 601 5.0
35 テッカグヤ はがね ひこう 207 199 219 600 6.5
36 ニダンギル はがね ゴースト 188 206 153 596 8.0
37 ゾウドウ はがね 140 91 176 594 14.0
38 メガクチート はがね フェアリー 188 217 137 593 8.0
39 クチート はがね フェアリー 155 141 137 590 12.0
40 メガボスゴドラ はがね 247 331 172 590 5.0
ひこう
Name type1 type2 ATK DEF HP rADH500 rADH500_PL
1 ホーホー ノーマル ひこう 67 88 155 705 33.5
2 チルット ノーマル ひこう 76 132 128 696 25.5
3 レディバ むし ひこう 72 118 120 693 29.0
4 バルジーナ あく ひこう 129 205 242 688 9.0
5 ハネッコ くさ ひこう 67 94 111 684 42.0
6 ワタッコ くさ ひこう 118 183 181 674 12.0
7 レディアン むし ひこう 107 179 146 672 15.0
8 コアルヒー みず ひこう 84 96 158 672 24.0
9 ポポッコ くさ ひこう 91 120 146 669 21.0
10 ミツハニー むし ひこう 59 83 102 669 50.0
11 メテノ(流星) いわ ひこう 116 194 155 669 13.0
12 バルチャイ あく ひこう 105 139 172 667 16.0
13 タマンタ みず ひこう 105 179 128 665 16.0
14 トロピウス くさ ひこう 136 163 223 658 10.0
15 ルギア エスパー ひこう 193 310 235 651 5.5
16 チルタリス ドラゴン ひこう 141 201 181 649 9.5
17 モクロー くさ ひこう 102 99 169 649 19.0
18 ヨルノズク ノーマル ひこう 145 156 225 643 9.5
19 マンタイン みず ひこう 148 226 163 642 9.0
20 エアームド はがね ひこう 148 226 163 642 9.0
21 アーマーガア ひこう はがね 163 192 221 640 8.0
22 ズバット どく ひこう 83 73 120 636 32.0
23 グライガー じめん ひこう 143 184 163 636 10.5
24 オンバット ひこう ドラゴン 83 73 120 636 32.0
25 ビークイン むし ひこう 149 190 172 633 9.5
26 ポッポ ノーマル ひこう 85 73 120 632 30.5
27 トゲチック フェアリー ひこう 139 181 146 630 11.5
28 フワンテ ゴースト ひこう 117 80 207 627 16.5
29 コロモリ エスパー ひこう 107 85 163 625 19.5
30 ヤヤコマ ノーマル ひこう 95 80 128 625 25.5
31 フクスロー くさ ひこう 142 139 186 625 11.0
32 フリーザー こおり ひこう 192 236 207 624 6.5
33 ピジョン ノーマル ひこう 117 105 160 623 16.5
34 マメパト ノーマル ひこう 98 80 137 622 24.0
35 ココガラ ひこう 88 67 116 620 31.5
36 アオガラス ひこう 129 110 169 618 14.5
37 カモネギ ノーマル ひこう 124 115 141 614 16.0
38 グライオン じめん ひこう 185 222 181 613 7.0
39 ピジョット ノーマル ひこう 166 154 195 612 9.0
40 ゴルバット どく ひこう 161 150 181 607 9.5